Тьюринг-полнота

Говорят, что задача является Тьюринг-полной, если её можно решить, используя только машину Тьюринга или любую систему, являющуюся Тьюринг-эквивалентной.

Определение:

Вычислительное устройство является Тьюринг-эквивалентным, если оно может эмулировать машину Тьюринга.

Зачастую Тьюринг-эквивалентные языки программирования называют Тьюринг-полными.

В теории вычислимости исполнитель (множество вычисляющих элементов) называется Тьюринг-полным, если на нём можно реализовать любую вычислимую функцию. Другими словами, для каждой вычислимой функции существует вычисляющий её элемент (например, машина Тьюринга) или программа для исполнителя, а все функции, вычисляемые множеством вычислителей, являются вычислимыми функциями (возможно, при некотором кодировании входных и выходных данных).

Любой полный по Тьюрингу язык достаточно универсальный, чтобы имитировать все другие (хотя и с потенциальным замедлением в работе). Такие языки эквивалентны в рамках вычислений, которые могут произвести. Полные по Тьюрингу языки настолько распространены, что их можно обнаружить даже в примитивных на первый взгляд системах, например, клеточных автоматах или мозаичных системах.

На практике полнота по Тьюрингу — идеализация. Компьютеры имеют ограниченное количество памяти и будут работать ограниченное количество времени, прежде чем их выключат.

Критерии Тьюринг-полноты

Если на языке программирования можно реализовать машину Тьюринга, то такой язык Тьюринг-полон, и наоборот. Возможность реализации машины Тьюринга на конкретном языке программирования можно грубо описать как перечень требований, которым этот язык должен для этого удовлетворять:

• Конечность (нет бесконечных символьных множеств и пр.)

• Фиксированное описание

• Всегда достаточный объём доступной памяти — в идеале здесь имеется в виду бесконечная память, однако физические рамки не позволяют сделать память ЭВМ бесконечной, поэтому она просто должна быть "always big enough".

• Неограниченность времени выполнения

• Возможность функциональной композиции (вызов одной функции из другой, рекурсия)

• Циклы while с прерыванием или эквивалентные им

• Возможность останавливать выполнение (halt) или каким-то образом подавать сигнал о результатах выполнения

• Представление множества натуральных чисел, понятие "следующее число". Возможны другие подобные системы.

• Поддержка входных и выходных данных (I/O), причём без ограничений в объёме. Если любая программа, написанная на каком-то языке программирования, принимает на вход не более фиксированного n бит данных и возвращает не более n бит, этот язык не может быть Тьюринг-полным.

Тьюринг-полнота и неполнота некоторых языков программирования

Доказать Тьюринг-полноту языка программирования можно, предложив способ реализации машины Тьюринга на этом языке. Кроме того, можно предложить интерпретатор языка на другом Тьюринг-полном языке.

Assembly language

Язык Ассемблера сильно ограничен: он рассчитан на архитектуру с конечной памятью и работает с конечным набором регистров. Однако, не был бы он полным по Тьюрингу, не были бы Тьюринг-полны и другие языки программирования.

Всё необходимое для машины Тьюринга на asm можно сделать примерно так:

 ADDS r0, r0, #1 ; сдвиг ленты вправо
 ADDS r0, r0, #-1 ; сдвиг ленты влево
 ADDS [r0], [r0], #1 ; инкремент значения, на которое "указывает" головка ленты
 ADDS [r0], [r0], #-1 ; декремент значения, на которое "указывает" головка ленты

И далее использовать инструкцию BEQ или ей подобную, чтобы выполнять определённую последовательность команд при определённом текущем значении, таким образом обеспечив ветвление.

Pascal

Язык Pascal позволяет смоделировать ленту машины Тьюринга с помощью двунаправленного списка из переменных, создаваемых оператором new, семантика которого не предполагает отказа в создании переменной. Также с помощью списков можно смоделировать сколь угодно большие числа. Стандарт не накладывает никаких ограничений: указательный тип абстрактен, множество значений указательного типа языком не ограничено. В Паскале есть еще один тип данных с неограниченным множеством значений, файловый, также пригодный для моделирования ленты машины Тьюринга и представления больших чисел. Достаточно утверждений для очевидности Тьюринг-полноты языка Pascal.

C

В языке C нет высокоуровневого понятия переменной (в смысле Паскаля), есть объекты (object), хранящиеся в памяти как последовательно расположенные байты,имеющие адрес (байты в свою очередь состоят из неадресуемых битов). Целые типы ограничены (конечное множество значений), указатель отождествляется с адресом, постулируется возможность хранить адрес в целочисленной переменной (int или long — зависит от реализации), откуда следует ограниченность множества значений указателей, а стало быть, и ограниченность адресного пространства C-машины. То есть язык C, как и язык ассемблера, ориентирован на архитектуру с конечной памятью. Файл не является типом данных языка C, в отличие от Паскаля. Это вещь из окружения, для работы с которой есть операции над потоками в виде набора библиотечных функций. Тип fpos_t, принятый в стандарте C для позиционирования файлов, постулируется как «отличный от массива тип данных (object type)». Следовательно, множество значений этого типа конечно, а значит, максимальная длина файла в языке C ограничена сверху.

SQL

Сам по себе SQL не считается полным по Тьюрингу языком. Однако, у него существует множество расширений, позволяющих делать рекурсивные запросы, циклы, списки, деревья и пр. Например, реализация решений некоторых известных задач с помощью PostgreSQL 8.4. Тем не менее, всё ещё остаётся ограниченное query execution time.

HTML

HTML можно назвать языком программирования только в контексте формальной полемики. На деле он является языком гипертекстовой разметки и ни чем больше. Т. е. на HTML можно совершить только некоторую ограниченную совокупность действий, интерпретируемых браузером, однако никто не запрещает сделать язык, идентичный по синтаксису с HTML, но интерпретируемый совершенно по другому таким образом, чтобы он был полным по Тьюрингу.

Некоторые другие ЯП

Название языка	Год изобретения	Парадигма	Уровень	Машинно-зависимость	Полнота по Тьюрингу
C	1972	Процедурный	Низкий	зав. от ISO	Да
C++	1983	Мультипарадигменный	Высокий/Низкий	Нет	Да
Язык Ассемблера	1950	Полнофункциональный	Низкий	Да	Да
SQL	1989	Декларативный	Высокий	Нет	Нет
Haskell	1990	Функциональный	Высокий	Нет	Да
HTML	1986	Декларативный	Высокий	Нет	Нет
CSS	1996	Декларативный	Высокий	Нет	Нет
Java	1995	Объектно-ориентированный	Высокий	Нет	Да
JavaScript	1965	Объектно-ориентированный	Высокий	Нет	Да
Python	1991	Объектно-ориентированный	Высокий	Нет	Да
XML	1998	Декларативный	Высокий	Нет	Нет
Brainfuck	1993	Эзотерический	Низкий	Да	Да
Whitespace	2003	Эзотерический	Низкий	Да	Да

Интересные случаи полноты по Тьюрингу

Шаблоны C++

Шаблоны C++ позволяют производить сложные вычисления ещё на стадии компиляции программы. Впервые это было продемонстрировано Эрвином Унрухом, который реализовал рекурсивный алгоритм распознавания простых чисел в процессе компиляции. Позже в статье Университета Индиана было продемонстрировано кодирование машины Тьюринга в шаблонах C++.

Java Generics

Аналогично C++ Templates, Generics, несмотря на свои отличия, тоже оказались полными по Тьюрингу, что было подтверждено Раду Григор в одной из статей Кентского Университета.

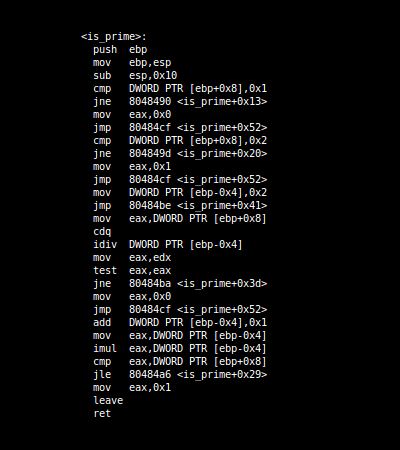
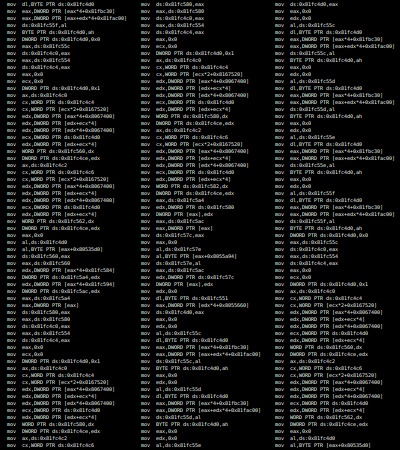
mov

Утилита M/o/Vfuscator превращает любую программу на языке C в огромную последовательность из инструкций mov.

Результат работы GCC

Результат работы M/o/Vfuscator

Простые числа с использованием одной инструкции

HTML5 + CSS3

Нововведения новых версий HTML/CSS позволяют построить правило 110, которое является Тьюринг-полным.

Тьюринговская трясина

Тьюринговская трясина — жаргонное общее название для языков программирования, которые Тьюринг-полны, но обладают крайне примитивными синтаксисом и семантикой. Они неудобны для практического программирования (из-за трудности написания программ и низкой производительности), зато хорошо подходят для некоторых других задач (доказательство невычислимости некоторых функций, иллюстрация базовых принципов программирования и т. д.). Поэтому они интересны для информатики.

Первыми представителями "трясины" были лямбда-исчисление, комбинаторная логика и сама машина Тьюринга.

Многие эзотерические языки программирования также являются «трясинами Тьюринга» (напр. Brainfuck, Spoon, Malbolge, Whitespace).

См. также

Машина Тьюринга

Источники информации

• Cunningham & Cunningham, Inc. — Turing Complete

• Stackexchange — What makes a language Turing-complete?

• Википедия — Тьюринговская трясина

• Википедия — Полнота по Тьюрингу

• А. А. Вылиток. Об алгоритмической полноте некоторых языков программирования

• «Умные контракты»: полнота по Тьюрингу и реальность

• Хабрахабр — Является ли HTML языком программирования?

• Andreas Zwinkau — Accidentially Turing-complete

• SNES Code Injection -- Flappy Bird in SMW