Хеширование кукушки

Пример хеширования кукушки. Стрелки показывают второе возможное место элементов. Если нам надо будет вставить новый элемент на место А, то мы поместим А в его вторую ячейку, занятую В, а В переместим в его вторую ячейку, которая сейчас свободна. А вот помещение нового элемента на место Н не получится: так как Н — часть цикла, добавленный элемент будет вытеснен после прохода по циклу.

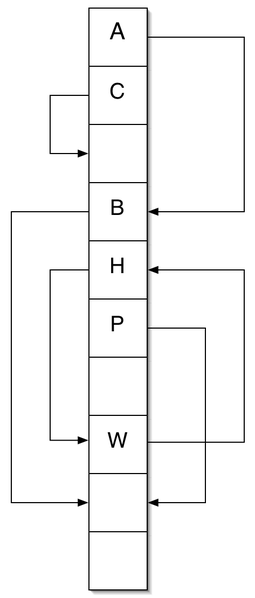
Хеширование кукушки(англ. Cuckoo hashing) — один из способов борьбы с коллизиями при создании хеш-таблицы.

Алгоритм

Основная идея хеширования кукушки — использование двух хеш-функций вместо одной (далее [math]h_1(x)[/math] и [math]h_2(x)[/math]). Также есть вариант алгоритма, в котором используются две хеш-таблицы, и первая хеш-функция указывает на ячейку из первой таблицы, а вторая — из второй. Рассмотрим алгоритмы функций add(x), remove(x) и contains(x).

Выберем [math]2[/math] хэш-функции [math]h_1(x)[/math] и [math]h_2(x)[/math] (из универсального семейства хэш-функций).

Add

Добавляет элемент с ключом [math]x[/math] в хэш-таблицу

1. Если одна из ячеек с индексами [math]h_1(x)[/math] или [math]h_2(x)[/math] свободна, кладем в нее элемент.
2. Иначе произвольно выбираем одну из этих ячеек, запоминаем элемент, который там находится, помещаем туда новый.
3. Смотрим в ячейку, на которую указывает другая хеш-функция от элемента, который запомнили, если она свободна, помещаем его в нее.
4. Иначе запоминаем элемент из этой ячейки, кладем туда старый. Проверяем, не зациклились ли мы.
5. Если не зациклились, то продолжаем данную процедуру поиска свободного места пока не найдем свободное место или зациклимся.
6. Иначе выбираем [math]2[/math] новые хеш-функции и перехешируем все добавленные элементы.
7. Так же после добавления нужно увеличить размер таблицы в случае если она заполнена.

Remove

Удаляет элемент с ключом [math]x[/math] из хэш-таблицы.

1. Смотрим ячейки с индексами [math]h_1(x)[/math] и [math]h_2(x)[/math].
2. Если в одной из них есть искомый элемент, просто помечаем эту ячейку как свободную.

Contains

Проверяет на наличие элемента [math]x[/math] в хэш-таблице

1. Смотрим ячейки с индексами [math]h_1(x)[/math] и [math]h_2(x)[/math].
2. Если в одной из них есть искомый элемент, возвращаем true.
3. Иначе возвращаем false.

Зацикливание

Зацикливание может возникнуть при добавлении элемента. Пусть мы добавляем элемент [math]x[/math]. И обе ячейки [math]h_1(x)[/math] и [math]h_2(x)[/math] заняты. Пусть, элемент [math]x[/math] положили в ячейку [math]h_i(x)[/math]. Если в ходе перемещений элементов в таблице на очередном шаге мы опять хотим переместить элемент [math]x[/math] в ячейку [math]h_i(x)[/math], чтобы в ячейку [math]h_j(x) ~(i \ne j) [/math] поместить какой-то [math]y[/math] (это может произойти, если в ходе перемещений элемент [math]x[/math] был перемещен в ячейку [math]h_j(x)[/math]), то произошло зацикливание.

Например зацикливание возникнет если добавить в хэш-таблицу [math]3[/math] элемента [math]x,y,z[/math] у которых [math]h_1(x)=h_1(y)=h_1(z)[/math] и [math]h_2(x)=h_2(y)=h_2(z)[/math] .

Одним из способов решения проблемы зацикливания является смена хэш-функции, что было доказано Джоном Трампом

Время работы алгоритма

Удаление и проверка происходят за [math]O(1)[/math] (что является основной особенностью данного типа хеширования), добавление в среднем происходит за [math]O(1)[/math]. Первые два утверждения очевидны: требуется проверить всего лишь [math]2[/math] ячейки таблицы.

Утверждение:

Добавление в среднем происходит за [math]O(1)[/math].

[math]\triangleright[/math]

Один из способов доказательства данного утверждения использует теорию случайных графов. Это делается через неориентированный "кукушкин граф", где каждой ячейке хеш-таблицы соответствует ровно одна вершина, а каждому добавленному элементу — ребро с концами в вершинах, соответствующих ячейкам, в которые указывают хеш-функции элемента. При этом элемент будет добавлен без перехеширования тогда и только тогда, когда после добавления нового ребра граф будет оставаться псевдолесом, то есть каждая его компонента связности будет содержать не более одного цикла.

[math]\triangleleft[/math]

Таким образом хеширование кукушки является одним из самых быстрых способов хеширования.

Плюсы и минусы алгоритма

Есть другие алгоритмы, которые используют несколько хеш-функций, в частности фильтр Блума, эффективная по памяти структура данных для нечётких множеств. Альтернативная структура данных для задач с теми же нечёткими множествами, основанная на кукушкином хешировании, называемая кукушкиным фильтром, использует даже меньшую память и (в отличие от классических фильтров Блума) позволяет удаление элемента, не только вставку и проверку существования. Однако теоретический анализ этих методов проведён существенно слабее, чем анализ фильтров Блума.

Исследования, проведённые Жуковским, Хеманом и Бонзом, показали, что кукушкино хеширование существенно быстрее метода цепочек для малых хеш-таблиц, находящихся в кэше современных процессоров. Кеннет Росс показал блочную версию кукушкиного хеширования (блок содержит более одного ключа), который работает быстрее обычных методов для больших хеш-таблиц в случае высокого коэффициента загрузки. Скорость работы блочной версии кукушкиной хеш-таблицы позднее исследовал Аскитис по сравнению с другими схемами кэширования.

Обзор Мутцемахера представляет открытые проблемы, связанные с кукушкиным хешированием.

См. также

• Хеш-таблица
• Разрешение коллизий
• Идеальное хеширование

Источники информации

• Wikipedia — Cuckoo hashing
• Cuckoo hashing — Pagh, Rasmus; Rodler, Flemming Friche (2001) (PDF, PS)

Примеры

• Concurrent high-performance Cuckoo hashtable written in C++
• Cuckoo hash map written in C++
• Static cuckoo hashtable generator for C/C++
• Generic Cuckoo hashmap in Java
• Cuckoo hash table written in Haskell
• Cuckoo hashing for Go