Rope — различия между версиями
Shersh (обсуждение | вклад) м (→Псевдокод) |
Heatwave (обсуждение | вклад) м (Отсыпал запятых, пофиксил немного орфографии) |
||
| Строка 1: | Строка 1: | ||
'''Rope''' (рус. ''веревка'') {{---}} структура данных для хранения строки, представляющая из себя двоичное сбалансированное дерево и позволяющая делать операции вставки, удаления и конкатенации с логарифмической асимптотикой. | '''Rope''' (рус. ''веревка'') {{---}} структура данных для хранения строки, представляющая из себя двоичное сбалансированное дерево и позволяющая делать операции вставки, удаления и конкатенации с логарифмической асимптотикой. | ||
| − | Иногда | + | Иногда при использовании строк нам нужны следующие свойства: |
| − | *Операции которые часто используются на строках, должны быть более эффективными. Например: конкатенация, взятие подстроки. | + | *Операции, которые часто используются на строках, должны быть более эффективными. Например: конкатенация, взятие подстроки. |
| − | *Также эти операции должны эффективно работать и с длинными строками. Не должно быть прямой зависимости от | + | *Также эти операции должны эффективно работать и с длинными строками. Не должно быть прямой зависимости от длины строк. |
*Персистентность. Иногда необходимо при изменении строки сохранить ее состояние перед изменением и вернуться к нему, если необходимо. | *Персистентность. Иногда необходимо при изменении строки сохранить ее состояние перед изменением и вернуться к нему, если необходимо. | ||
| Строка 9: | Строка 9: | ||
==Описание структуры== | ==Описание структуры== | ||
| − | Для хранения Rope создадим структуру, похожую на [[Декартово дерево по неявному ключу|декартово дерево по неявному ключу]]. В каждом листе будем хранить последовательную часть строки и ее длину, а в промежуточных вершинах будем хранить сумму длин всех листьев в поддереве. Изначально дерево состоит из одной вершины {{---}} | + | Для хранения Rope создадим структуру, похожую на [[Декартово дерево по неявному ключу|декартово дерево по неявному ключу]]. В каждом листе будем хранить последовательную часть строки и ее длину, а в промежуточных вершинах будем хранить сумму длин всех листьев в поддереве. Изначально дерево состоит из одной вершины {{---}} самой строки. Используя информацию в промежуточных вершинах, можно получать символы строки по индексу, как будет показано ниже. Также заметим, что для отметки листа не обязательно хранить дополнительную информацию: все внутренние вершины имеют ровно двух детей, а листы {{---}} ни одного. Поэтому для проверки вершины на то, что она является листом, достаточно проверить, есть ли у неё дети. |
==Merge== | ==Merge== | ||
| − | Когда приходит запрос на конкатенацию с другой строкой мы объединяем оба дерева, создав новый корень и подвесив к нему обе строки. | + | Когда приходит запрос на конкатенацию с другой строкой, мы объединяем оба дерева, создав новый корень и подвесив к нему обе строки. |
Пример результата конкатенации двух строк: | Пример результата конкатенации двух строк: | ||
| Строка 23: | Строка 23: | ||
===Время работы=== | ===Время работы=== | ||
| − | Асимптотика выполнения операции конкатенации двух строк очевидно <tex>O(1)</tex>. | + | Асимптотика выполнения операции конкатенации двух строк, очевидно, <tex>O(1)</tex>. |
==Получение символа по индексу== | ==Получение символа по индексу== | ||
| − | Чтобы получить символ по некоторому индексу <tex>i</tex>, будем спускаться по дереву из корня, используя веса записанные вершинах чтобы определить в какое поддерево пойти из текущей вершины. Алгоритм выглядит следующим образом: | + | Чтобы получить символ по некоторому индексу <tex>i</tex>, будем спускаться по дереву из корня, используя веса, записанные в вершинах, чтобы определить, в какое поддерево пойти из текущей вершины. Алгоритм выглядит следующим образом: |
* Текущая вершина {{---}} не лист, тогда возможно два варианта: | * Текущая вершина {{---}} не лист, тогда возможно два варианта: | ||
** Вес левого поддерева больше либо равен <tex>i</tex>, тогда идем в левое поддерево. | ** Вес левого поддерева больше либо равен <tex>i</tex>, тогда идем в левое поддерево. | ||
** Иначе идем в правое поддерево и ищем там <tex>i - w</tex> символ, где <tex>w</tex> вес левого поддерева. | ** Иначе идем в правое поддерево и ищем там <tex>i - w</tex> символ, где <tex>w</tex> вес левого поддерева. | ||
| − | * Текущая вершина {{---}} лист, тогда в этом листе хранится ответ | + | * Текущая вершина {{---}} лист, тогда в этом листе хранится ответ; необходимо взять символ с соответствующим номером у строки, которая там хранится. |
===Псевдокод=== | ===Псевдокод=== | ||
| Строка 46: | Строка 46: | ||
===Время работы=== | ===Время работы=== | ||
| − | Асимптотика выполнения одного такого запроса очевидно <tex>O(h)</tex>, где <tex>h</tex> {{---}} высота дерева. | + | Асимптотика выполнения одного такого запроса, очевидно, <tex>O(h)</tex>, где <tex>h</tex> {{---}} высота дерева. |
==Split== | ==Split== | ||
| − | Чтобы разбить строку на две по некоторому индексу <tex>i</tex> необходимо спускаясь по дереву (аналогично операции <tex>\mathrm{get}</tex>), каждую вершину на пути поделить на две, каждая из которых будет соответствовать | + | Чтобы разбить строку на две по некоторому индексу <tex>i</tex>, необходимо, спускаясь по дереву (аналогично операции <tex>\mathrm{get}</tex>), каждую вершину на пути поделить на две, каждая из которых будет соответствовать одной из половинок строк, при этом необходимо после деления пересчитать вес этих вершин. |
Пускай дано дерево: | Пускай дано дерево: | ||
| Строка 60: | Строка 60: | ||
[[file:Split2.png|800px|Результат выполнения операции split.]] | [[file:Split2.png|800px|Результат выполнения операции split.]] | ||
| − | Заметим, что появляются лишние вершины, у которых есть только один потомок. От них можно легко | + | Заметим, что появляются лишние вершины, у которых есть только один потомок. От них можно легко избавиться, просто заменив их на этого потомка. Тогда результатом той же операции <tex>\mathrm{split}</tex> будет: |
[[file:Split3.png|800px|Результат выполнения операции split.]] | [[file:Split3.png|800px|Результат выполнения операции split.]] | ||
| Строка 89: | Строка 89: | ||
===Время работы=== | ===Время работы=== | ||
| − | Нетрудно заметить что асимптотическая сложность выполнения данной операции <tex>O(h)</tex>, где <tex>h</tex> {{---}} высота дерева. | + | Нетрудно заметить, что асимптотическая сложность выполнения данной операции {{---}} <tex>O(h)</tex>, где <tex>h</tex> {{---}} высота дерева. |
==Операции удаления и вставки== | ==Операции удаления и вставки== | ||
| − | Нетрудно понять, что имея | + | Нетрудно понять, что имея операции <tex>\mathrm{merge}</tex> и <tex>\mathrm{split}</tex>, можно легко через них выразить операции <tex>\mathrm{delete}</tex> и <tex>\mathrm{insert}</tex> по аналогии с другими деревьями поиска. |
| − | Операция <tex>\mathrm{delete}</tex> удаляет из строки подстроку начиная с индекса <tex>beginIndex</tex> и заканчивая (не включая) индексом <tex>endIndex</tex>. | + | Операция <tex>\mathrm{delete}</tex> удаляет из строки подстроку, начиная с индекса <tex>beginIndex</tex> и заканчивая (не включая) индексом <tex>endIndex</tex>. |
===Псевдокод=== | ===Псевдокод=== | ||
| Строка 103: | Строка 103: | ||
'''return''' merge(tree1, tree3) | '''return''' merge(tree1, tree3) | ||
| − | Операция <tex>\mathrm{insert}</tex> вставляет данную строку <tex>s</tex> в исходную начиная с позиции <tex>insertIndex</tex>. | + | Операция <tex>\mathrm{insert}</tex> вставляет данную строку <tex>s</tex> в исходную, начиная с позиции <tex>insertIndex</tex>. |
===Псевдокод=== | ===Псевдокод=== | ||
| Строка 113: | Строка 113: | ||
===Время работы=== | ===Время работы=== | ||
| − | Так как данные операции используют только <tex>\mathrm{split}</tex> и <tex>\mathrm{merge}</tex> то асимптотика времени их работы <tex>O(h)</tex>, где <tex>h</tex> {{---}} высота дерева. | + | Так как данные операции используют только <tex>\mathrm{split}</tex> и <tex>\mathrm{merge}</tex>, то асимптотика времени их работы {{---}} <tex>O(h)</tex>, где <tex>h</tex> {{---}} высота дерева. |
==Балансировка== | ==Балансировка== | ||
| − | Для того чтобы дерево не превращалось в бамбук: | + | Для того, чтобы дерево не превращалось в бамбук: |
[[file:Bamboo.png|800px|Пример вырождения дерева в бамбук.]] | [[file:Bamboo.png|800px|Пример вырождения дерева в бамбук.]] | ||
| Строка 125: | Строка 125: | ||
==Оптимизации== | ==Оптимизации== | ||
| − | * Для уменьшения объема памяти занимаемой деревом и уменьшения высоты дерево, предлагается при конкатенации с маленькой строкой делать конкатенацию классическим способом. | + | * Для уменьшения объема памяти, занимаемой деревом, и уменьшения высоты дерево, предлагается при конкатенации с маленькой строкой делать конкатенацию классическим способом. |
| − | * Кэширование. Так как зачастую нужен последовательный доступ к индексам (например <tex>i</tex> и <tex>i + 1</tex>), то можно запоминать лист | + | * Кэширование. Так как зачастую нужен последовательный доступ к индексам (например <tex>i</tex> и <tex>i + 1</tex>), то можно запоминать лист (а также его границы), в который мы пришли после очередного запроса <tex>\mathrm{get}</tex>, и на следующем запросе сначала искать в сохраненном листе. Также если хранить у каждой вершины ее предка, то последовательный доступ к символам будет выполняться за <tex>O(m)</tex>, где <tex>m</tex> {{---}} количество символов. |
==См. также== | ==См. также== | ||
Версия 01:07, 10 февраля 2018
Rope (рус. веревка) — структура данных для хранения строки, представляющая из себя двоичное сбалансированное дерево и позволяющая делать операции вставки, удаления и конкатенации с логарифмической асимптотикой.
Иногда при использовании строк нам нужны следующие свойства:
- Операции, которые часто используются на строках, должны быть более эффективными. Например: конкатенация, взятие подстроки.
- Также эти операции должны эффективно работать и с длинными строками. Не должно быть прямой зависимости от длины строк.
- Персистентность. Иногда необходимо при изменении строки сохранить ее состояние перед изменением и вернуться к нему, если необходимо.
В данном случае Rope удовлетворяет всем этим свойствам.
Содержание
Описание структуры
Для хранения Rope создадим структуру, похожую на декартово дерево по неявному ключу. В каждом листе будем хранить последовательную часть строки и ее длину, а в промежуточных вершинах будем хранить сумму длин всех листьев в поддереве. Изначально дерево состоит из одной вершины — самой строки. Используя информацию в промежуточных вершинах, можно получать символы строки по индексу, как будет показано ниже. Также заметим, что для отметки листа не обязательно хранить дополнительную информацию: все внутренние вершины имеют ровно двух детей, а листы — ни одного. Поэтому для проверки вершины на то, что она является листом, достаточно проверить, есть ли у неё дети.
Merge
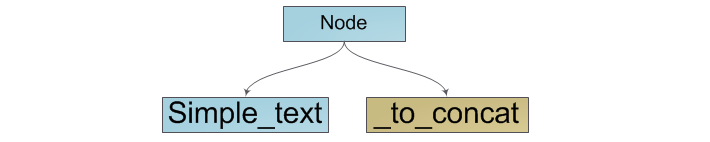
Когда приходит запрос на конкатенацию с другой строкой, мы объединяем оба дерева, создав новый корень и подвесив к нему обе строки. Пример результата конкатенации двух строк:
Псевдокод
Node merge(Node n1, Node n2):
return Node(n1, n2, n1.w + n2.w)
Время работы
Асимптотика выполнения операции конкатенации двух строк, очевидно, .
Получение символа по индексу
Чтобы получить символ по некоторому индексу , будем спускаться по дереву из корня, используя веса, записанные в вершинах, чтобы определить, в какое поддерево пойти из текущей вершины. Алгоритм выглядит следующим образом:
- Текущая вершина — не лист, тогда возможно два варианта:
- Вес левого поддерева больше либо равен , тогда идем в левое поддерево.
- Иначе идем в правое поддерево и ищем там символ, где вес левого поддерева.
- Текущая вершина — лист, тогда в этом листе хранится ответ; необходимо взять символ с соответствующим номером у строки, которая там хранится.
Псевдокод
char get(int i, Node node):
if node.left
if node.left.w >= i
return get(i, node.left)
else
return get(i - node.left.w, node.right)
else
return node.s[i]
Время работы
Асимптотика выполнения одного такого запроса, очевидно, , где — высота дерева.
Split
Чтобы разбить строку на две по некоторому индексу , необходимо, спускаясь по дереву (аналогично операции ), каждую вершину на пути поделить на две, каждая из которых будет соответствовать одной из половинок строк, при этом необходимо после деления пересчитать вес этих вершин.
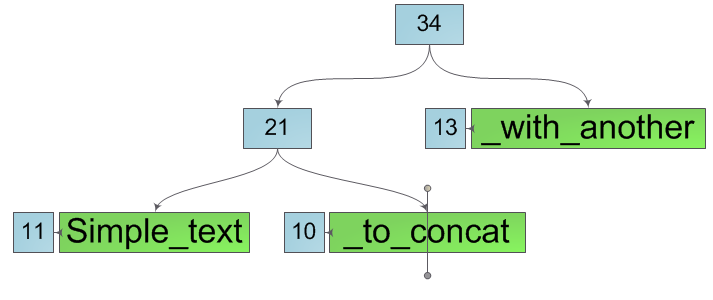
Пускай дано дерево:
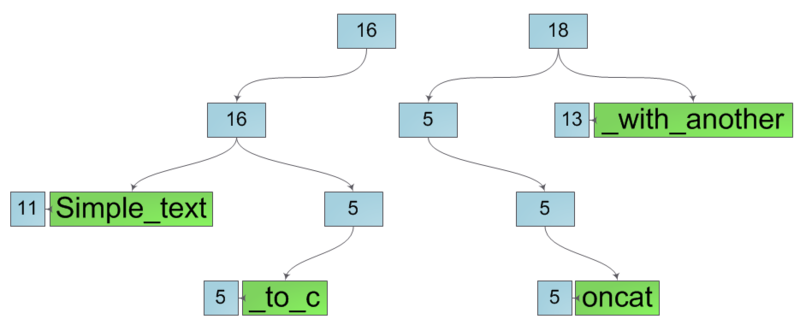
Тогда результатом выполнения операции по индексу будет:
Заметим, что появляются лишние вершины, у которых есть только один потомок. От них можно легко избавиться, просто заменив их на этого потомка. Тогда результатом той же операции будет:
Псевдокод
Pair<Node, Node> split(Node node, int i):
Node tree1, tree2
if node.left
if node.left.w >= i
res = split(node.left, i)
tree1 = res.first
tree2.left = res.second
tree2.right = node.right
tree2.w = tree2.left.w + tree2.right.w
else
res = split(node.right, i - node.left.w)
tree1.left = node.left
tree1.right = res.first
tree1.w = tree1.left.w + tree1.right.w
tree2 = res.second
else
tree1.s = node.s.substr(0, i)
tree2.s = node.s.substr(i, node.s.len)
tree1.w = i
tree2.w = node.s.len - i
return tree1, tree2
Время работы
Нетрудно заметить, что асимптотическая сложность выполнения данной операции — , где — высота дерева.
Операции удаления и вставки
Нетрудно понять, что имея операции и , можно легко через них выразить операции и по аналогии с другими деревьями поиска.
Операция удаляет из строки подстроку, начиная с индекса и заканчивая (не включая) индексом .
Псевдокод
Node delete(Node node, int beginIndex, int endIndex):
(tree1, tree2) = split(node, beginIndex)
tree3 = split(tree2, endIndex - beginIndex).second
return merge(tree1, tree3)
Операция вставляет данную строку в исходную, начиная с позиции .
Псевдокод
Node insert(Node node, int insertIndex, string s):
(tree1, tree3) = split(node, insertIndex)
tree2 = Node(s)
return merge(merge(tree1, tree2), tree3)
Время работы
Так как данные операции используют только и , то асимптотика времени их работы — , где — высота дерева.
Балансировка
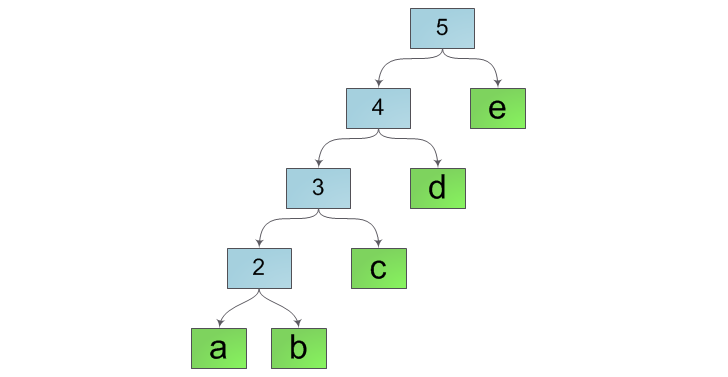
Для того, чтобы дерево не превращалось в бамбук:
Предлагается хранить его как АВЛ-дерево и делать соответствующие балансировки. Тогда, так как высота АВЛ-дерева , то асимптотика операций будет равна , где — количество сконкатенированных строк.
Оптимизации
- Для уменьшения объема памяти, занимаемой деревом, и уменьшения высоты дерево, предлагается при конкатенации с маленькой строкой делать конкатенацию классическим способом.
- Кэширование. Так как зачастую нужен последовательный доступ к индексам (например и ), то можно запоминать лист (а также его границы), в который мы пришли после очередного запроса , и на следующем запросе сначала искать в сохраненном листе. Также если хранить у каждой вершины ее предка, то последовательный доступ к символам будет выполняться за , где — количество символов.