Асимптотика гипергеометрических последовательностей

Определение:

Последовательность, в которой отношение двух соседних членов равно отношению многочленов степени [math]n[/math], где [math]n \gt 0[/math], называется гипергеометрической (англ. hypergeometric sequence).

Вычисление асимптотики

Лемма:

Пусть последовательность [math]a_0, a_1, \ldots[/math] положительных чисел такова, что [math]\cfrac{a_{n+1}}{a_n}=A\cfrac{n^k+\alpha_1 n^{k-1}+ \ldots +\alpha_k}{n^k+\beta_1 n^{k-1}+ \ldots +\beta_k}[/math] для всех достаточно больших [math]n[/math], причем [math]\alpha_1 \ne \beta_1[/math]. Тогда [math]a_n[/math] растет как [math]a_n \sim cA^n n^{\alpha_1-\beta_1}[/math] для некоторой постоянной [math]c\gt 0[/math].

Доказательство:

[math]\triangleright[/math]

Утверждение леммы эквивалентно тому, что существует предел [math]\lim\limits_{n \to \infty} {\cfrac{a_n}{A^n n^{\alpha_1-\beta_1}}}[/math]. Прологарифмировав, мы приходим к необходимости доказать существование предела [math]\lim\limits_{n \to \infty} { \ln {a_n} - n \ln A - (\alpha_1 - \beta_1)\ln n }[/math]. Для доказательства существования предела применим критерий Коши, т. е. будем доказывать, что рассматриваемая последовательность фундаментальна. Фундаментальность последовательности означает, что для любого [math]ε \gt 0[/math] существует такой номер [math]N[/math], что для всех [math]n \gt N[/math] и всех положительных [math]m[/math] [math]|\ln {a_{n+m}} - \ln {a_n} - (n+m) \ln A + n \ln A - (\alpha_1 - \beta_1)\ln(n+m)+(\alpha_1-\beta_1)\ln n| \lt ε[/math] или [math]|\ln {a_{n+m}} - \ln {a_n} - m \ln A - (\alpha_1 - \beta_1) \ln {(n+m)} + (\alpha_1-\beta_1) \ln n| \lt ε (*)[/math] Перепишем отношение [math]\cfrac{a_{n+1}}{a_n}[/math] в виде [math]\cfrac{a_{n+1}}{a_n}=A\cfrac{1+\alpha_1 n^{-1} + \ldots + \alpha_k n^{-k}}{1+\beta_1 n^{-1} + \ldots + \beta_k n^{-k}}=Af(\cfrac{1}{n})[/math], где [math]f(x)=\cfrac{1+\alpha_1 x + \ldots + \alpha_k x^k}{1+\beta_1 x + \ldots + \beta_k x^k}[/math] Прологарифмировав отношение [math]\cfrac{a_{n+1}}{a_n}[/math], получаем [math]\ln a_{n+1} - \ln a_n = \ln A + \ln f(\cfrac{1}{n})[/math]. Посмотрим на функцию [math]\ln f(x)[/math]. Выпишем начальные члены разложения функции [math]f[/math] в ряд в точке [math]0[/math]: [math]f(x)=1 + (\alpha_1 - \beta_1)x + \gamma x^2 + \ldots[/math] для некоторой константы [math]\gamma[/math]. Это разложение - самый существенный элемент доказательства. Именно коэффициент [math]\alpha_1 - \beta_1[/math](отличный от нуля по предположению леммы) при линейном члене указывает на присутствие сомножителя [math]n^{\alpha_1-\beta_1}[/math] в асимптотике. Для логарифма функции [math]f[/math] имеем [math]\ln f(x)=(\alpha_1-\beta_1)x+\tilde{\gamma}x^2 + \ldots[/math] Поэтому для некоторой постоянной [math]C[/math] при достаточно маленьком [math]x[/math] имеем [math]|\ln f(x) = (\alpha_1 - \beta_1)x|\lt Cx^2[/math]. В частности, если [math]N[/math] достаточно велико, то [math]∀ n\gt N[/math] [math]|\ln a_{n+1} - \ln a_n - \ln A - (\alpha_1 - \beta_1) \cfrac{1}{n}|\lt C \cfrac{1}{n^2}[/math], [math]|\ln a_{n+2} - \ln a_{n+1} - \ln A - (\alpha_1 - \beta_1) \cfrac{1}{n+1}|\lt C \cfrac{1}{(n+1)^2}[/math], [math]\ldots[/math] [math]|\ln a_{n+m} - \ln a_{n+m-1} - \ln A - (\alpha_1 - \beta_1) \cfrac{1}{n+m}|\lt C \cfrac{1}{(n+m)^2}[/math]. Теперь интересующее нас выражение в левой части неравенства [math](*)[/math] можно оценить с помощью системы и неравенства треугольника: [math]| \ln a_{n+m} - \ln a_n - m \ln A - (\alpha_1 - \beta_1)( \ln {(n+m)} - \ln n)| =[/math] [math]= | \ln a_{n+m} - \ln a_{n + m - 1} + \ln a_{n + m - 1} - \ldots + \ln a_{n + 1} - \ln a_n - m \ln A - [/math] [math] - (\alpha_1 - \beta_1) \sum\limits_{k=0}^{m-1} \cfrac{1}{n+k} + (\alpha_1 - \beta_1) \sum\limits_{k=0}^{m-1} \cfrac{1}{n+k} - (\alpha_1 - \beta_1)(\ln {(n+m)} - \ln n)| \leqslant[/math] [math]\leqslant | \ln a_{n+1} - \ln a_n - \ln A - (\alpha_1 - \beta_1) \cfrac{1}{n} | + | \ln a_{n+2} - \ln a_{n+1} - \ln A - (\alpha_1 - \beta_1) \cfrac{1}{n+1}| +[/math] [math]\ldots[/math] [math]+ | \ln a_{n+m} - \ln a_{n+m-1} - \ln A - (\alpha_1 - \beta_1) \cfrac{1}{n+m}| + | \alpha_1 - \beta_1 | | \sum\limits_{k=0}^{m-1} \cfrac{1}{n+k} - \ln {(n+m)} + \ln n | \leqslant[/math] [math]\leqslant C(\cfrac{1}{n^2} + \cfrac{1}{(n+1)^2} + \ldots + \cfrac{1}{(n+m-1)^2}) + | \alpha_1 - \beta_1 | | \sum\limits_{k=0}^{m-1} \cfrac{1}{n+k} - \ln {(n+m)} + \ln n |[/math]. 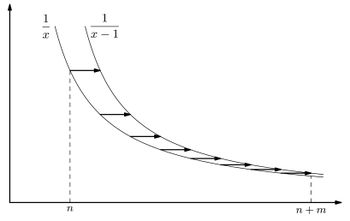Поскольку ряд [math]\sum\limits_{k=1}^{\infty} \cfrac{1}{k^2}[/math] сходится, первое слагаемое в правой части последнего неравенства при больших [math]n[/math] можно сделать сколь угодно малым. Чтобы оценить второе слагаемое, заметим, что стоящая в нем сумма представляет собой площадь под графиком ступенчатой функции [math]\cfrac{1}{[x]}[/math] на отрезке [math][n, n+m][/math], График функции [math]y = \cfrac{1}{[x]}[/math] на отрезке [math][n, n + m][/math] (Здесь через [math][x][/math] обозначена целая часть числа [math]x[/math], наибольшее целое число, не превосходящее [math]x[/math].) Эта площадь больше, чем площадь под графиком функции [math]y = \cfrac{1}{x}[/math], но меньше, чем площадь под графиком функции [math]y = \cfrac{1}{x-1}[/math] на этом же отрезке. Площадь под графиком функции [math]y = \cfrac{1}{x-1}[/math] равна [math]\ln {(n+m-1)} - \ln {(n-1)}[/math]. Таким образом, интересующая нас разность не превосходит [math]|(\ln {(n+m-1)} - \ln {(n-1)}) - (- \ln {(n+m)} + \ln n)| = | \ln {(1 - \cfrac{1}{n+m})} - \ln {(1 - \cfrac{1}{n})}| \lt |\ln {(1 - \cfrac{1}{n})}| \lt C \cfrac{1}{n}[/math].

[math]\triangleleft[/math]

Замечание: Предположения леммы не позволяют определить величину константы [math]c[/math]. Действительно, умножив последовательность [math]a_n[/math] на произвольную постоянную [math]d \gt 0[/math], мы получим новую последовательность с тем же отношением последовательных членов, константа [math]c[/math] для которой увеличивается в [math]d[/math] раз

Примеры

Пример. Для чисел Каталана имеем

[math]\cfrac{c_{n+1}}{c_n}=\cfrac{4n+2}{n+2}=4\cfrac{n+\cfrac{1}{2}}{n+2}[/math]

Поэтому [math]c_n \sim c \cdot 4^n \cdot n^{-\frac{3}{2}}[/math] для некоторой постоянной [math]c[/math].

Пример. Найдем асимптотику коэффициентов для функции [math](a-s)^{\alpha}[/math], где [math]\alpha[/math] вещественно. В ряде случаев эта асимптотика нам уже известна, например, при [math]\alpha=−1[/math]. Согласно определению функции [math](1-s)^{\alpha}[/math] имеем

[math](a-s)^{\alpha}=a^{\alpha}(1-\cfrac{s}{a})^{\alpha}=a^{\alpha}(1 - \cfrac{\alpha}{1!} \cfrac{s}{a} + \cfrac{\alpha(\alpha-1)}{2!}{(\cfrac{s}{a})^2} - \cfrac{\alpha(\alpha-1)(\alpha-2)}{3!}(\cfrac{s}{a})^3 + \ldots)[/math].

Если [math]\alpha[/math] — целое неотрицательное число, то ряд обрывается и вопроса об асимптотике не возникает. В противном случае начиная с некоторого номера все коэффициенты ряда имеют одинаковый знак. Для определения асимптотики мы можем воспользоваться леммой при [math]a_n=(-1)^n \cfrac{\alpha(\alpha-1) \ldots (\alpha-n+1)}{n!{\alpha}^n}[/math]

[math]\cfrac{a_{n+1}}{a_n}=\cfrac{1}{a} \cfrac{n-\alpha}{n+1}[/math]

Поэтому [math]a_n \sim c \cdot a^{-n} \cdot n^{-\alpha-1}[/math]. Например, коэффициенты функции [math]-(1-4s)^{\frac{1}{2}}[/math] ведут себя как [math]c \cdot 4^n \cdot n^{-\frac{3}{2}}[/math], и мы получаем повторный вывод ассимптотики для чисел Каталана.

См. также

• Производящая функция

Источники информации

• Ландо С.А., Лекции о производящих функциях, 2007 год