Проблема четырёх красок — различия между версиями
Mervap (обсуждение | вклад) (→Общие идеи доказательства) |
Mervap (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
{{Теорема | {{Теорема | ||
|about= | |about= | ||
| Строка 9: | Строка 5: | ||
}} | }} | ||
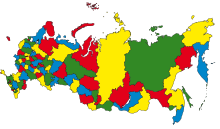
[[Файл:Map of Russia(four colour).png|230px|thumb|right|Карта России раскрашенная в <tex>4</tex> цвета]] | [[Файл:Map of Russia(four colour).png|230px|thumb|right|Карта России раскрашенная в <tex>4</tex> цвета]] | ||
| − | |||
| − | Поэтому | + | == Общие идеи доказательства == |
| + | Проблема четырех красок на первый взгляд выглядит мало связанной с другими разделами математики и практическими задачами.Однако известно более <tex>20</tex> ее переформулировок, которые связывают эту проблему с задачами алгебры, статистической механики и задачами планирования. | ||
| + | |||
| + | Поэтому начнем с того, что заменим задачу раскраски плоской карты на эквивалентную ей проблему. Выберем столицу у каждой страны и соединим дугами столицы стран, имеющих общий сегмент границы. В результате получится [[Укладка графа на плоскости|планарный граф]]. Тогда следующая теорема эквивалентна теореме выше: | ||
{{Теорема | {{Теорема | ||
|about= | |about= | ||
| Строка 19: | Строка 17: | ||
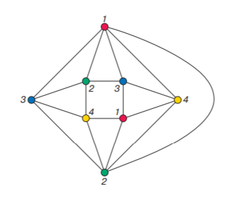
[[Файл:Раскраска_планарного_графа_в_4_цвета.png|230px|thumb|right|4-раскраска планарного графа]] | [[Файл:Раскраска_планарного_графа_в_4_цвета.png|230px|thumb|right|4-раскраска планарного графа]] | ||
| − | + | В таком виде в <tex>1977</tex> году проблема четырех красок была доказана К. Аппелем и У. Хакеном и опубликована в двух статьях <ref>Appel K., Haken W. Every Planar Map Is Four Colorable. Contemporary Mathematics. Providence (R.I.): Amer. Math Soc., 1989. Vol. 98. 308 р.</ref>. Значительную часть проверок выполнил компьютер, из-за чего доказательство было принято не всеми математиками. Дело в том, что даже сами авторы доказательства пишут следующее: | |
''"Читатель должен разобраться в <tex>50</tex> страницах текста и диаграмм, <tex>85</tex> страницах с почти <tex>2500</tex> дополнительными диаграммами, <tex>400</tex> страницами микрофишей, содержащими еще диаграммы, а также тысячи отдельных проверок утверждений, сделанных в <tex>24</tex> леммах основного текста. Вдобавок читатель узнает, что проверка некоторых фактов потребовала <tex>1200</tex> часов компьютерного времени, а при проверке вручную потребовалось бы гораздо больше. Статьи устрашающи по стилю и длине, и немногие математики прочли их сколько-нибудь подробно"'' | ''"Читатель должен разобраться в <tex>50</tex> страницах текста и диаграмм, <tex>85</tex> страницах с почти <tex>2500</tex> дополнительными диаграммами, <tex>400</tex> страницами микрофишей, содержащими еще диаграммы, а также тысячи отдельных проверок утверждений, сделанных в <tex>24</tex> леммах основного текста. Вдобавок читатель узнает, что проверка некоторых фактов потребовала <tex>1200</tex> часов компьютерного времени, а при проверке вручную потребовалось бы гораздо больше. Статьи устрашающи по стилю и длине, и немногие математики прочли их сколько-нибудь подробно"'' | ||
| − | + | Очевидно, что из-за сложности доказательства мы не сможем рассмотреть его целиком, но посмотрим на общие идеи, которые в нем используются. | |
| − | + | Во-первых, если [[Укладка графа на плоскости|грани]] образованные нашим планарным графом не триангуляция (то есть имеют не ровно три ребра у их границ), мы можем добавлять ребра без внедрения новых вершин до тех пор, пока все грани не станут триангулированными. Если полученный граф является раскрашиваемым в не более чем <tex>4</tex> цвета, то и исходный граф раскрашиваем так же (так как удаление ребер не увеличивает хроматическое число). Поэтому достаточно доказать теорему для триангулированных графов, и без потери общности мы предполагаем, что граф триангулирован. | |
| − | |||
| − | |||
| − | Во-первых, если [[Укладка графа на плоскости|грани]] образованные нашим планарным графом не триангуляция | ||
Для дальнейших рассуждений нам понадобится следующее утверждение: | Для дальнейших рассуждений нам понадобится следующее утверждение: | ||
| Строка 37: | Строка 32: | ||
}} | }} | ||
| − | Из данного утверждения следует, что в графе существует вершина степени <tex>\leqslant | + | Из данного утверждения следует, что в графе существует вершина степени не больше <tex>5</tex>. |
| + | |||
| + | Попытаемся доказать теорему от противного. Пусть у нас существует граф, который требует хотя бы <tex>5</tex> цветов для раскраски. Среди всех таких графов существует минимальный, то есть такой граф <tex>G</tex>, что удаление любой вершины из него делает его <tex>4</tex>-раскрашиваемым. | ||
| + | |||
| + | {{Утверждение | ||
| + | |statement=В <tex>G~\nexists </tex> вершины <tex>v \in V</tex> : <tex>dev(v) \leqslant 4</tex> | ||
| + | |proof=Если в <tex>G</tex> есть вершина степени <tex>3</tex>, то мы можем просто удалить ее из графа, раскрасить полученный граф в <tex>4</tex> цвета, вернуть удаленную вершину и покрасить ее в один из цветов, не занятых соседями. Аналогично [[Хроматическое_число_планарного_графа#Раскраска_в_5_цветов|теореме Хивуда]] доказывается, что удалив вершину степени <tex>4</tex> также всегда можно раскрасить граф в <tex>4</tex> цвета. | ||
| + | }} | ||
| − | + | Для вершины степени <tex>5</tex> аналогичное утверждение неверно, хотя оно и присутствовало в одном из первых ошибочных доказательств. | |
| − | На этом этапе мы | + | На этом этапе мы натыкаемся на самую сложную часть доказательства. Имея дело со случаем вершины степени <tex>5</tex>, нельзя просто удалить ее. Тогда вместо <tex>1</tex> вершины будем рассматривать связанный подграф из нескольких вершин (назовем его '''конфигурацией'''). Тогда для некоторых случаев, как и прежде, достаточно продемонстрировать, что если при удалении конфигурации граф <tex>4</tex>-раскрашиваемый, то окраска может быть изменена таким образом, что при возвращении конфигурации граф также можно раскрасить в <tex>4</tex> цвета. Конфигурации для которых это возможно назовем '''сводимыми'''. Например, конфигурация состоящая из <tex>1</tex> вершины степени <tex>\leqslant 4</tex> является сводимой (было доказано выше). '''Неизбежной''' конфигурацией назовем такое '''множество''' конфигураций, что хотя бы одна из конфигураций этого множества обязана быть в нашем графе. |
Если нам удастся найти какую-то неизбежную конфигурацию и доказать, что с ней граф все равно <tex>4</tex>-раскрашиваем, доказательство будет завершено. Основным методом, используемым, чтобы обнаружить такой набор, является [https://en.wikipedia.org/wiki/Discharging_method_(discrete_mathematics) метод разгрузки] | Если нам удастся найти какую-то неизбежную конфигурацию и доказать, что с ней граф все равно <tex>4</tex>-раскрашиваем, доказательство будет завершено. Основным методом, используемым, чтобы обнаружить такой набор, является [https://en.wikipedia.org/wiki/Discharging_method_(discrete_mathematics) метод разгрузки] | ||
| Строка 63: | Строка 65: | ||
== Источники информации == | == Источники информации == | ||
* [https://www.youtube.com/watch?v=ysbqis1qofM Лекция Thomas Fernique] | * [https://www.youtube.com/watch?v=ysbqis1qofM Лекция Thomas Fernique] | ||
| − | |||
* [https://en.wikipedia.org/wiki/Four_color_theorem Four color theorem] | * [https://en.wikipedia.org/wiki/Four_color_theorem Four color theorem] | ||
* [https://en.wikipedia.org/wiki/Discharging_method_(discrete_mathematics) Discharging method] | * [https://en.wikipedia.org/wiki/Discharging_method_(discrete_mathematics) Discharging method] | ||
Версия 18:40, 12 ноября 2018
| Теорема (Проблема четырех красок): |
Теорема о четырёх красках — утверждение о том, что всякую карту можно раскрасить четырьмя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета. Под общим участком границы понимается часть линии, то есть стыки нескольких областей в одной точке общей границей для них не считаются. |
Общие идеи доказательства
Проблема четырех красок на первый взгляд выглядит мало связанной с другими разделами математики и практическими задачами.Однако известно более ее переформулировок, которые связывают эту проблему с задачами алгебры, статистической механики и задачами планирования.
Поэтому начнем с того, что заменим задачу раскраски плоской карты на эквивалентную ей проблему. Выберем столицу у каждой страны и соединим дугами столицы стран, имеющих общий сегмент границы. В результате получится планарный граф. Тогда следующая теорема эквивалентна теореме выше:
| Теорема (Хроматическое число планарного графа): |
Хроматическое число планарного графа не превосходит . |
В таком виде в году проблема четырех красок была доказана К. Аппелем и У. Хакеном и опубликована в двух статьях [1]. Значительную часть проверок выполнил компьютер, из-за чего доказательство было принято не всеми математиками. Дело в том, что даже сами авторы доказательства пишут следующее:
"Читатель должен разобраться в страницах текста и диаграмм, страницах с почти дополнительными диаграммами, страницами микрофишей, содержащими еще диаграммы, а также тысячи отдельных проверок утверждений, сделанных в леммах основного текста. Вдобавок читатель узнает, что проверка некоторых фактов потребовала часов компьютерного времени, а при проверке вручную потребовалось бы гораздо больше. Статьи устрашающи по стилю и длине, и немногие математики прочли их сколько-нибудь подробно"
Очевидно, что из-за сложности доказательства мы не сможем рассмотреть его целиком, но посмотрим на общие идеи, которые в нем используются.
Во-первых, если грани образованные нашим планарным графом не триангуляция (то есть имеют не ровно три ребра у их границ), мы можем добавлять ребра без внедрения новых вершин до тех пор, пока все грани не станут триангулированными. Если полученный граф является раскрашиваемым в не более чем цвета, то и исходный граф раскрашиваем так же (так как удаление ребер не увеличивает хроматическое число). Поэтому достаточно доказать теорему для триангулированных графов, и без потери общности мы предполагаем, что граф триангулирован.
Для дальнейших рассуждений нам понадобится следующее утверждение:
| Утверждение: |
Для триангулированного графа , где — количество вершин степени , а — максимальная степень вершины в графе. |
| Так как граф триангулирован, то , где — количество ребер, а — количество граней. Из формулы Эйлера |
Из данного утверждения следует, что в графе существует вершина степени не больше .
Попытаемся доказать теорему от противного. Пусть у нас существует граф, который требует хотя бы цветов для раскраски. Среди всех таких графов существует минимальный, то есть такой граф , что удаление любой вершины из него делает его -раскрашиваемым.
| Утверждение: |
В вершины : |
| Если в есть вершина степени , то мы можем просто удалить ее из графа, раскрасить полученный граф в цвета, вернуть удаленную вершину и покрасить ее в один из цветов, не занятых соседями. Аналогично теореме Хивуда доказывается, что удалив вершину степени также всегда можно раскрасить граф в цвета. |
Для вершины степени аналогичное утверждение неверно, хотя оно и присутствовало в одном из первых ошибочных доказательств.
На этом этапе мы натыкаемся на самую сложную часть доказательства. Имея дело со случаем вершины степени , нельзя просто удалить ее. Тогда вместо вершины будем рассматривать связанный подграф из нескольких вершин (назовем его конфигурацией). Тогда для некоторых случаев, как и прежде, достаточно продемонстрировать, что если при удалении конфигурации граф -раскрашиваемый, то окраска может быть изменена таким образом, что при возвращении конфигурации граф также можно раскрасить в цвета. Конфигурации для которых это возможно назовем сводимыми. Например, конфигурация состоящая из вершины степени является сводимой (было доказано выше). Неизбежной конфигурацией назовем такое множество конфигураций, что хотя бы одна из конфигураций этого множества обязана быть в нашем графе.
Если нам удастся найти какую-то неизбежную конфигурацию и доказать, что с ней граф все равно -раскрашиваем, доказательство будет завершено. Основным методом, используемым, чтобы обнаружить такой набор, является метод разгрузки
Приведем пример нахождения неизбежной конфигурации:
| Утверждение: |
В планарном графе есть вершина степени или конфигурация состоящая из вершин степени или из вершины степени и степени |
| Присвоим каждой вершине некую величину — груз . Предположим что наше утверждение неверно. Следовательно, в графе нет вершин степени . Тогда положительный груз есть только у вершин степени (и он равен единице), у вершин степени груз , а у всех остальных он отрицательный. По доказанному выше утверждению, мы знаем что сумма грузов по всем вершинам . Значит вершины степени должны компенсировать все отрицательные грузы других вершин. Пусть каждая такая вершина отдает по своего груза соседям. Тогда у всех вершин степени и груз останется равен (помним что вершины степени не смежны с вершинами степени по предположению). Рассмотрим все остальные вершины. Так как мы проводим доказательство для триангулированных графов, то у вершины степени не может быть больше чем соседей степени . Однако для , следовательно, сумма грузов отрицательна. Получено противоречие. |
Выше мы получили неизбежную конфигурацию, состоящую из небольшого количество элементов. Подобными действиями Аппель и Хакен провели операций разгрузки и получили неизбежную конфигурацию из конфигураций. Некоторые из них являются сводимыми, доказательством раскрашиваемости графов с остальными и занимался компьютер.
См. также
Примeчания
- ↑ Appel K., Haken W. Every Planar Map Is Four Colorable. Contemporary Mathematics. Providence (R.I.): Amer. Math Soc., 1989. Vol. 98. 308 р.