Мультиплексор и демультиплексор

Эта статья находится в разработке!

Определение:

Мультиплексор (англ. multiplexer, или mux) - логический элемент, получающий на вход [math]2^n[/math] булевых значений; [math]n[/math]-значное число [math]x[/math] в двоичном представлении и возвращающий значение на [math]x[/math]-м входе.

Определение:

Демультиплексор (англ. demultiplexer, или demux) - логический элемент, получающий на вход булево значение [math]z[/math]; [math]n[/math]-значное число [math]x[/math] в двоичном представлении и выводящий [math]z[/math] на [math]x[/math]-й из своих [math]2^n[/math] выходов. На все остальные выходы элемент выдаёт [math]0[/math].

Принцип работы мультиплексора

2-to-1 мультиплексор

4-to-1 мультиплексор

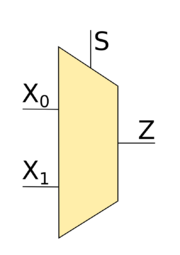
Рассмотрим мультиплексор 2-to-1 (это значит, что есть всего два входа $X_0$ и $X_1$, значения которых могут подаваться на вход $Z$). Рассмотрим всевозможные варианты значений на входах. Если на $S$ подавать $0$, то на выход $Z$ будет подаваться то же значение, которое подаётся на вход $X_0$, т.е. в данном случае значение на входе $X_1$ нас не интересует. Аналогично, если на вход $S$ подавать $1$, то на выход $Z$ будет подаваться то же значение, которое подаётся на вход $X_1$. Для более лучшего понимания посмотрим на таблицу истинности.

$S$	$X_0$	$X_1$	$Z$
0	0	?	0
0	1	?	1
1	?	0	0
1	?	1	1

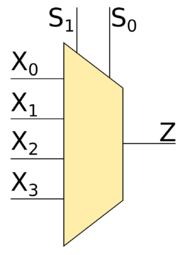
Также рассмотрим мультиплексор 4-to-1 (это значит, что есть четыре входа $X_0$, $X_1$, $X_2$ и $X_3$, значения которых могут подаваться на выход $Z$). Также рассмотрим всевозможные варианты значений на входах. Тут уже 2 входа $S_0$ и $S_1$, которые определяют, значение какого из входов $X_)$, $X_1$, $X_2$ или $X_3$ будет подаваться на выход $Z$. Если $S_0 = S_1 = 0$, то на выход $Z$ будет подаваться значение входа $X_0$, если $S_0 = 1$ и $S_1 = 0$ - то значение $X_1$, если $S_0 = 0$ и $S_1 = 1$ - то значение $X_2$, в противном случае - значение $X_3$. Для более лучшее понимания рекомендуется обратиться к таблице истинности.

$S_0$	$S_1$	$X_0$	$X_1$	$X_2$	$X_3$	$Z$
0	0	0	?	?	?	0
0	0	1	?	?	?	1
1	0	?	0	?	?	0
1	0	?	1	?	?	1
0	1	?	?	0	?	0
0	1	?	?	1	?	1
1	1	?	?	?	0	0
1	1	?	?	?	1	1

Логическая схема мультиплексора

Логическая схема мультиплексора 4-to-1

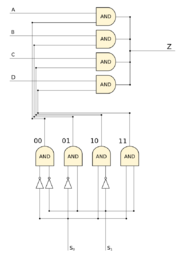
Построим логическую схему мультиплексора. Очевидно, что если входы $s_0$, $s_1$, $\ldots$, $s_{n-1}$ задают вход $x_i$, причем значение на входе $x_i$ равно $0$, то на выходе $z$ будет $0$, если же значение на входе $x_i$ равно $1$, то и на выходе $z$ значение тоже будет $1$. Также давайте построим логическую схему, которая перебирает всевозможные варианты значений на входах $s_0$, $s_1$, $\ldots$, $s_{n-1}$, т.е. имеет $n$ входов и $2^n$ выходов, причём на всех выходах будет $0$ кроме $i$-ого выхода, на котором будет $1$, где $i$ - число, которое кодируется входами. Такая схема называется шифратором, и подробное её устройство можно почитаться в соответствующей статье, размер такой схемы будет $O(2^n)$. Теперь давайте соединим гейтами $AND$ вход $x_i$ и выход $i$ шифратора, а получившиеся провода от гейтов $AND$ мы все сведём к выходу $Z$. Очевидно, что такая схема будет иметь размер, линейно зависящий от количества входов.

Принцип работы демультиплексора

Рассмотрим демультиплексор 1-to-2 (это значит, что у демультиплексора два выхода). Если на вход $S$ подать значение $0$, то на выход $z_0$ будет подаваться то же значение, которое подаётся на вход $y$, а на выход $z_1$ будет подаваться $0$. Если же на вход $s$ подать значение $1$, то на выход $z_0$ будет подаваться значение $0$, а на выход $z_1$ то же значение, которое будет подаваться на вход $y$. Для более лучшего понимания посмотрим на таблицу истинности.

$S$	$Y$	$Z_0$	$Z_1$
0	0	0	0
0	1	1	0
1	0	0	0
1	1	0	1

Также рассмотрим демультиплексор 1-to-4 (это значит, что у демультиплексора четыре выхода). Теперь у нас уже есть два входа $s_0$ и $s_1$, которые определяют, на какой из выходов $z_0$, $z_1$, $z_2$ или $z_3$ будет подаваться значение $y$, тогда как на остальные выходы будет подаваться $0$. В случае, когда $s_0 = s_1 = 0$, то на выход $z_0$ будет подаваться значение на входе $y$, тогда как на $z_1$, $z_2$ и $z_3$ будет подаваться $0$. Если же $s_0 = 1$ и $s_1 = 0$, то на выходы $z_0$, $z_2$ и $z_3$ будет подаваться $0$, а на выход $z_1$ будет подаваться то же, что подаётся на вход $y$. Аналогично разбираются остальные случаи. Для более лучшего понимания посмотрим на таблицу истинности.

$S_0$	$S_1$	$Y$	$Z_0$	$Z_1$	$Z_2$	$Z_3$
0	0	0	0	0	0	0
0	0	1	1	0	0	0
1	0	0	0	0	0	0
1	0	1	0	1	0	0
0	1	0	0	0	0	0
0	1	1	0	0	1	0
1	1	0	0	0	0	0
1	1	1	0	0	0	1

Логическая схема демультиплексора

Логическая схема мультиплексора 1-to-4

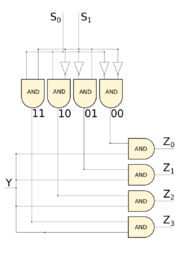
Построим схему для демультиплексора. С помощью дешифратора преобразуем входы $s_0$, $s_1$, $\ldots$, $s_{n-1}$ в $2^n$ проводов $y_0$, $y_1$, $\ldots$, $y_{2^n-1}$, причем на проводе $y_i$ будет $1$, если число $i$ кодируется входами $s_0$, $s_1$, $\ldots$, $s_{n-1}$, в противном случае на проводе $y_i$ будет значение $0$. Потом каждый из этих проводов соединим со входом $y$ с помощью гейта $AND$, и выходу $z_i$ будет соответствовать тот гейт $AND$, на вход которого подают провод $y_i$.

См. также

• Метод Лупанова синтеза схем
• Дешифратор

Источники информации

• Wikipedia - Multiplexer