Группы. Действие группы на множестве — различия между версиями
Perveevm (обсуждение | вклад) (→Источники информации) |
Perveevm (обсуждение | вклад) (→Орбита и стабилизатор) |
||
| Строка 37: | Строка 37: | ||
|definition=Пусть группа <tex>G</tex> действует на множество <tex>X</tex>. Тогда '''стабилизатором''' (англ. ''stabilizer'') элемента <tex>g \in G</tex> называется множество его неподвижных точек: <tex>St(g) = \{x \in X \mid g \cdot x = x\}</tex> | |definition=Пусть группа <tex>G</tex> действует на множество <tex>X</tex>. Тогда '''стабилизатором''' (англ. ''stabilizer'') элемента <tex>g \in G</tex> называется множество его неподвижных точек: <tex>St(g) = \{x \in X \mid g \cdot x = x\}</tex> | ||
}} | }} | ||
| + | |||
| + | {{Утверждение | ||
| + | |id=stab | ||
| + | |statement=<tex>Orb(x) \cap Orb(y) \neq \varnothing \Rightarrow Orb(x) = Orb(y)</tex> | ||
| + | |proof=<tex>Orb(x) \cap Orb(y) \neq \varnothing \Rightarrow \exists g_1, g_2 \in G : g_1 \cdot x = g_2 \cdot y \Rightarrow x = g_1^{-1} \cdot (g_2 \cdot y) = (g_1^{-1} \cdot g_2) \cdot y \Rightarrow x \in Orb(y)</tex> | ||
| + | |||
| + | Заметим, что <tex>\forall g \in G: g \cdot x \in Orb(y) \Rightarrow Orb(x) \subseteq Orb(y)</tex> | ||
| + | |||
| + | Аналогично доказывается, что <tex>Orb(y) \subseteq Orb(x)</tex> | ||
| + | |||
| + | Таким образом, <tex>Orb(x) = Orb(y)</tex> | ||
| + | }} | ||
| + | |||
{{Утверждение | {{Утверждение | ||
Версия 00:18, 27 декабря 2018
| Определение: |
Группа действует на множестве (англ. acts on a set) , если задано отображение (обозначается ), такое что для любого , а также для любых оно обладает свойствами:
|
Содержание
Эквивалентность по группе
| Определение: |
| Пусть группа действует на множестве . Введем на отношение эквивалентности для : , если . Тогда, если , то говорят, что и равны с точностью до группы. |
| Утверждение: |
Отношение является отношением эквивалентности. |
|
Орбита и стабилизатор
| Определение: |
| Пусть группа действует на множество . Тогда орбитой (англ. orbit) элемента называется множество: . Множество всех орбит обозначается так: . |
Иными словами, орбитой элемента множества в группе называется порожденный им класс эквивалентности по отношению . Задача подсчета количества классов эквивалентности является нетривиальной и решается в общем случае при помощи Леммы Бёрнсайда.
| Определение: |
| Элемент называется неподвижной точкой (англ. fixed point) элемента , если |
| Определение: |
| Пусть группа действует на множество . Тогда стабилизатором (англ. stabilizer) элемента называется множество его неподвижных точек: |
| Утверждение: |
|
Заметим, что Аналогично доказывается, что Таким образом, |
| Утверждение: |
Примеры
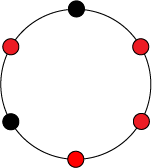
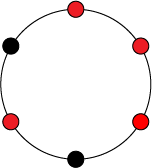
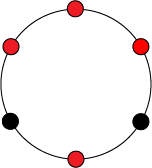
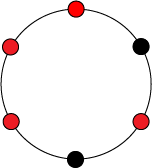
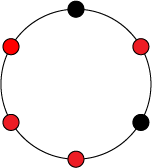
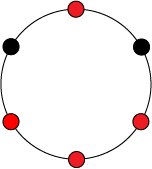
В качестве примера рассмотрим ожерелья, состоящие из бусин, которые бывают красного и черного цвета. Таким образом, множество — это множество всевозможных ожерелий из бусин, окрашенных в один из двух цветов. Теперь введем группу , в которой будет элементов: , где будет означать поворот ожерелья на угол против часовой стрелки.
Таким образом, правое ожерелье получено из левого путем действия на него элементом . Из этого следуют, что левое и правое ожерелья равны с точностью до группы , а значит они находятся в одном классе эквивалентности.
Теперь в качестве примера рассмотрим орбиту левого ожерелья — все элементы множества , полученные из элемента путем поворотов на различных углов.