Критерий Тарьяна минимальности остовного дерева — различия между версиями
Filchenko (обсуждение | вклад) (фикс) |
Filchenko (обсуждение | вклад) (зяпятушечки) |
||
| Строка 8: | Строка 8: | ||
Легко заметить, что остовное дерево, не удовлетворяющее условию, не минимально: | Легко заметить, что остовное дерево, не удовлетворяющее условию, не минимально: | ||
| − | Если существует ребро, не максимальное на образовавшемся цикле мы можем уменьшить вес дерева, добавив это ребро и удалив максимальное. | + | Если существует ребро, не максимальное на образовавшемся цикле, мы можем уменьшить вес дерева, добавив это ребро и удалив максимальное. |
| − | Теперь докажем, что дерево, удовлетворяющее условию минимально: | + | Теперь докажем, что дерево, удовлетворяющее условию, минимально: |
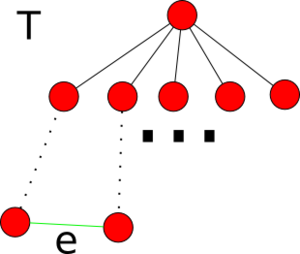
Обозначим дерево <tex>T</tex>, покажем что его можно построить алгоритмом Крускала. | Обозначим дерево <tex>T</tex>, покажем что его можно построить алгоритмом Крускала. | ||
Версия 20:29, 15 января 2011
| Теорема (критерий минимальности остовного дерева Тарьяна): |
Остовное дерево минимально тогда и только тогда, когда любое ребро не из дерева является максимальным на цикле, который образуется при его добавлении в дерево. |
| Доказательство: |
|
Легко заметить, что остовное дерево, не удовлетворяющее условию, не минимально: Если существует ребро, не максимальное на образовавшемся цикле, мы можем уменьшить вес дерева, добавив это ребро и удалив максимальное. Теперь докажем, что дерево, удовлетворяющее условию, минимально: Обозначим дерево , покажем что его можно построить алгоритмом Крускала. Индукция по количеству ребер в дереве: База: пустое дерево. Переход: Строим дерево по лемме о безопасном ребре. Рассмотрим минимальное невзятое ребро . Рассмотрим разрез, окружающий одну из двух компонент. Пусть не минимально в разрезе, тогда существует такое, что . Рассмотрим : некое ребро , такое что , будет лежать на цикле. Противоречие условию теоремы. Если минимально — добавим его в . В процессе индукции добавлялись только ребра из , поэтому построенное дерево совпадет с . |