Дерево решений и случайный лес — различия между версиями
Sokolova (обсуждение | вклад) |
Sokolova (обсуждение | вклад) |
||
| Строка 7: | Строка 7: | ||
'''Дерево решений''' (англ. ''decision tree, DT'') {{---}} алгоритм классификации <tex>a(x)</tex>, задающийся деревом (связным ациклическим графом): | '''Дерево решений''' (англ. ''decision tree, DT'') {{---}} алгоритм классификации <tex>a(x)</tex>, задающийся деревом (связным ациклическим графом): | ||
* Множество вершин <tex> V = V_{внутр} \cup V_{лист} </tex>, <tex>v_0 \in V</tex> {{---}} корень дерева | * Множество вершин <tex> V = V_{внутр} \cup V_{лист} </tex>, <tex>v_0 \in V</tex> {{---}} корень дерева | ||
| − | * Для <tex>v \in V_{внутр}</tex> определены функции: <tex> f_v : X \rightarrow D_v </tex> и <tex> D_v : X \rightarrow V </tex>, <tex>D_v < \infty</tex> | + | * Для <tex>v \in V_{внутр}</tex> определены функции: <tex> f_v : X \rightarrow D_v </tex> и <tex> D_v : X \rightarrow V </tex>, <tex>|D_v| < \infty</tex> |
* Для <tex>v \in V_{лист}</tex> определена метка класса <tex>y_v \in Y</tex> | * Для <tex>v \in V_{лист}</tex> определена метка класса <tex>y_v \in Y</tex> | ||
| + | }} | ||
| + | {{Определение | ||
| + | |id=def1 | ||
| + | |neat = | ||
| + | |definition= | ||
| + | '''Бинарное решающее дерево''' {{---}} частный случай дерева решений, для которого <tex> D_v = {0,1} </tex>. | ||
| + | * Пример <tex>f_v = [f_j(x) > a_j]</tex>, где <tex>f_j(x)</tex> - значение <tex>j</tex>-ого признака объекта <tex>x \in X</tex> | ||
}} | }} | ||
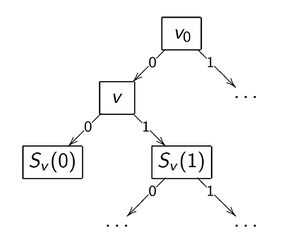
[[Файл:BinDT1.jpg |300px|thumb|right|Классификация объекта <tex> x \in X </tex> бинарным решающим деревом]] | [[Файл:BinDT1.jpg |300px|thumb|right|Классификация объекта <tex> x \in X </tex> бинарным решающим деревом]] | ||
| Строка 17: | Строка 24: | ||
<tex>v := S_v</tex>(<tex>f_v</tex>(x)) ; | <tex>v := S_v</tex>(<tex>f_v</tex>(x)) ; | ||
'''return''' <tex>y_v</tex> | '''return''' <tex>y_v</tex> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Версия 16:05, 20 января 2019
Содержание
Дерево решений
| Определение: |
Дерево решений (англ. decision tree, DT) — алгоритм классификации , задающийся деревом (связным ациклическим графом):
|
| Определение: |
Бинарное решающее дерево — частный случай дерева решений, для которого .
|
Y classify(x): while : ((x)) ; return
Основные определения
Простейший алгоритм синтеза дерева
Разновидности решающих деревьев
Тип задачи
Критерии ветвления
Критерии останова
Что находится во внутренних вершинах
Что находится в листьях
Передача информации между вершинами
- (alternating decision tree)
Рецукция решающих деревьев
Оценивание вероятностей
Полужадный синтез
Алгоритмы построения решающих деревьев
Обобщающая способность решающих деревьев
Композиции решающих деревьев
- Решающий лес
- Бустинг над решающими деревьями
История
Ссылки
- Classification and Regression Trees — лекции Cosma Shalizi, ноябрь 2009.