Блокирующий поток — различия между версиями
(Новая страница: «{{Определение |definition= <b>Блокирующий поток</b> - такой поток <tex>f</tex> в данной сети <tex>G</tex>, что л…») |
|||
| Строка 4: | Строка 4: | ||
}} | }} | ||
| − | Блокирующий поток не обязательно максимален. [[Теорема Форда-Фалкерсона]] говорит о том, что поток будет максимальным тогда и только тогда, когда в остаточной сети не найдётся <tex>s \leadsto t</tex> пути; в блокирующем же потоке ничего не утверждается о существовании пути по рёбрам, появляющимся в остаточной сети. | + | [[Файл:Блокпоток.png|thumb|right|Рис. 1]] |
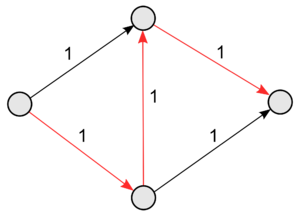
| + | Блокирующий поток не обязательно максимален (см. рис. 1). [[Теорема Форда-Фалкерсона]] говорит о том, что поток будет максимальным тогда и только тогда, когда в остаточной сети не найдётся <tex>s \leadsto t</tex> пути; в блокирующем же потоке ничего не утверждается о существовании пути по рёбрам, появляющимся в остаточной сети. | ||
== См. также == | == См. также == | ||
Версия 00:51, 16 января 2011
| Определение: |
| Блокирующий поток - такой поток в данной сети , что любой путь содержит насыщенное этим потоком ребро. Иными словами, в данной сети не найдётся такого пути из истока в сток, вдоль которого можно беспрепятственно увеличить поток. |
Блокирующий поток не обязательно максимален (см. рис. 1). Теорема Форда-Фалкерсона говорит о том, что поток будет максимальным тогда и только тогда, когда в остаточной сети не найдётся пути; в блокирующем же потоке ничего не утверждается о существовании пути по рёбрам, появляющимся в остаточной сети.