Теорема Фишера-Линча-Патерсона (FLP)

Теорема Фишера, Линча и Патерсона (FLP, 1985 год) невозможно достичь даже необоснованного консенсуса $N>2$ процессами даже на одном бите при следующих условиях:

• Алгоритм должен завершиться за конечное время.
• Один из узлов может отказать
• Система асинхронна
• Алгоритм должен быть детерминирован.

Если отказов нет, есть простой алгоритм. Если система синхронна, то есть консенсус в синхронных системах. Если разрешаем недетерминизм, то есть алгоритм Бен-Ора.

Доказательство

Из презентации Р. Елизарова.

От противного: пусть есть такой алгоритм, тогда мы проанализируем варианты его исполнения, подстроим порядок доставки сообщений (без откладывания сообщений бесконечно далеко), получим бесконечную цепочку выполнения и противоречие с конечностью алгоритма.

Модель

Определение:

Процесс — это детерминированный автомат, который может выполнять три операции: receive() : msg — бесконечная блокировка до получения ближайшего сообщения. Так как система асинхронна, возможности "посмотреть следующее сообщение" или таймаутов нет. send(msg) — отправка сообщения другому процессу. Гарантируется, что сообщение дойдёт получателю за конечное время, но это время может быть сколь угодно большим. decided(value) — процесс принял решение value. Решение процесс может принять только один раз, но после этого он может продолжить выполняться и помогать остальным процессам. Заметим, что так как нет "времени", можно считать все переходы в процессе мгновенными.

Для доказательства от противного у нас есть такой алгоритм для процессов, что все они вызывают decided(value) с одинаковым значением через конечное время, независимо от того, как система задерживает сообщения.

Определение:

Конфигурация — это состояния всех процессов плюс все сообщения в пути (которые отправили, но ещё не доставили).

В начальной конфигурация у каждого процесса может быть сколько угодно входных данных и даже своя программа. Начальных конфигураций может быть несколько, они могут отличаться, например, предложениями процессов.

Определение:

Шаг из одной конфигурации в другую — это приём какого-то сообщения процессом (событие) и последовавшие за этим внутренние действия процесса до следующего receive(). Эти действия однозначно определяются предыдущей конфигурацией и событием.

Определение:

Исполнение — это бесконечная цепочка шагов из какой-нибудь начальной конфигурации. Бесконечная, потому что процессы могут выполняться и после принятия решений.

Определение:

Отказавший процесс — это процесс, который делает только конечное количество шагов в исполнении. Такой в системе может быть максимум один (это более сильное условие, чем если может много процессов отказывать).

Также гарантируется, что в любом исполнении любое сообщение, предназначенное не отказавшему процессу, обрабатывается через конечное число шагов. Другими словами, сообщения не теряются.

Валентность

Заметим, что в любом исполнении всегда принимается решение. Даже если один процесс отказал, то все остальные должны прийти к решению за конечное число шагов.

Определение:

Конфигурация называется $i$-валентной и одновалентной, если все цепочки шагов из неё приводят к решению $i$. Таким образом, бывают 0-валентные и 1-валентные конфигурации. Если же из конфигурации есть цепочки, приводящие к каждому из решений, то такая конфигурация называется бивалентной.

Наблюдение: пусть из конфигурации $X$ есть цепочка шагов, обрабатывающая сообщения из $X$ в подмножестве процессов $A$, за которой идёт цепочка процессов, обрабатывающая сообщения из $X$ в подмножестве процессов $B$, и в конце мы получили конфигурацию $Y$. Тогда эти цепочки коммутируют: можно сначала обработать сообщения подмножеством процессов $B$, а потом — $A$ (так как мы обрабатываем только сообщения из $X$, а не новые).

Наблюдение: за $i$-валентной конфигурацией могут следовать только $i$-валентные.

Начальная бивалентная конфигурация

Лемма: существует бивалентная начальная конфигурация.

Доказательство от противного: пусть все начальные конфигурации одновалентны. Из нетривиальности консенсуса мы знаем, что есть как 0-, так и 1-валентные начальные конфигурации. Тогда можно найти две начальные конфигурации разной валентности, которые отличаются только состоянием одного процесса: взяли две произвольные начальные конфигурации разной валентности, начали переводить одну в другую копированием исходных состояний процессов, по одному процессу за шаг.

А раз есть две такие конфигурации разной валентности, то пусть в каждой из них этот процесс (где они отличаются) откажет с самого начала, до отправки и приёма любых сообщений. Тогда мы всё ещё получим консенсус, но решение будет одинаковым, потому что внешняя система никак не может выявить состояние отказавшего процесса. А они исходно были разной валентности, противоречие.

Цепочка бивалентных конфигураций

Лемма: для любой бивалентной конфигурации можно найти следующую за ней бивалентную.

Следствие: если лемма верна, то мы можем построить бесконечную цепочку бивалентных конфигураций и тем самым получим противоречие и докажем FLP: есть бесконечная цепочка, в которой не принято решение.

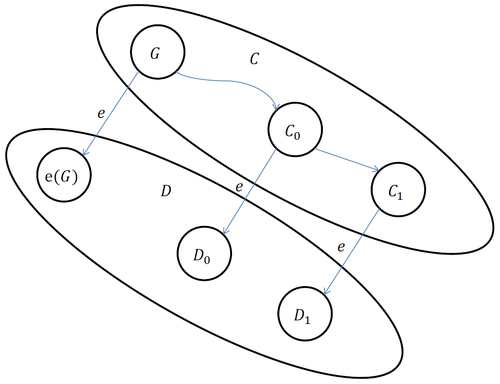
Доказательство: от противного. Пусть все конфигурации после некотороый бивалентной конфигурации $G$ одновалентны. Введём определения:

• $e$ — какое-то событие в $G$, скармливающее сообщение $m$ процессу $p$. Такое есть, иначе у нас в конфигурации ничего не происходит, она бивалентна, а решение должно быть детерминированным, противоречие.
• $C$ — множество конфигураций, достижимых из $G$ без использования $e$. В частности, в $C$ по предположению отсутствуют бивалентные конфигурации.
• $D=e(C)$, то есть все конфигурации, достижимые из $G$, где $e$ — последнее обработанное событие. В частности, в $D$ по предположению отсутствуют бивалентные конфигурации.

Теперь докажем, что $D$ содержит бивалентную конфигурацию. То есть мы выбрали, насколько сильно отложить обработку произвольного события $e$ и показали, что это не порушит бивалентность. Надо ещё аккуратно, чтобы это не порушило конечность обработки каждого сообщения. Например, их можно обрабатывать по очереди, начиная с самых старых. Тогда каждое событие рано или поздно попадёт в наш шаг и будет обработано.

Шаг 1: существование $i$-валентных конфигураций в $D$

Подлемма: для любого $i$ в $D$ существует $i$-валентная конфигурация.

В самом деле: так как $G$ бивалентна, то по какой-то цепочке шагов из неё можно дойти до $i$-валентной конфигурации $E_i$. Дальше разбором случаев находим искомую конфигурацию в $D$:

• Если $E_i \in D$, то мы доказали подлемму.
• Если $E_i \in C$, то $e(E_i) \in D$, у $e(E_i)$ такая же валентность и мы снова доказали подлемму.
• Иначе ребро $e$ применялось в цепочке шагов для достижения $E_i$ из $G$. Найдём конфигурацию $F_i \in D$, которая была в этой цепочке шагов сразу после применения $e$. Так как в $D$ нет бивалентных конфигураций, то $F_i$ является $i$-валентной, что и требовалось.

Ссылки

• http://bailonga.es/tpmtp/lecture09.pdf
• https://github.com/volhovm/study-notes/blob/master/parallel_programming/parallel_programming.org