Алгоритм Укконена — различия между версиями
Kot (обсуждение | вклад) (Новая страница: «{{В разработке}} ==Оптимизация алгоритма Укконена== {{Определение |definition= Пусть <tex>x\alpha</tex> об…») |
DrozdovVA (обсуждение | вклад) (алгоритм за O(n^3)) |
||
| Строка 1: | Строка 1: | ||
{{В разработке}} | {{В разработке}} | ||
| + | '''Алгоритм Укконена''' — алгоритм построения [[Сжатое суффиксное дерево|суффиксного дерева]] для заданной строки <tex>s</tex> за линейное время. | ||
| + | |||
| + | == Первая версия алгоритма == | ||
| + | Рассмотрим сначала метод, который строит дерево за время <tex>O(n^3)</tex>, где <tex>n</tex> — длина исходной строки <tex>s</tex>. В дальнейшем данный алгоритм будет оптимизирован таким образом, что будет достигнута линейная скорость работы. | ||
| + | |||
| + | === Описание === | ||
| + | Алгоритм делится на <tex>n</tex> фаз. В фазе с номером <tex>i</tex> в дерево добавляются все суффиксы подстроки <tex>s_{1..i}</tex>. При добавлении суффикса <tex>s_{j..i}</tex> алгоритм сначала находит конец пути из корня, помеченного подстрокой <tex>s_{j..i-1}</tex>, затем добавляет к концу этой подстроки очередной символ <tex>s_i</tex>, если этот символ не был добавлен ранее. | ||
| + | |||
| + | === Псевдокод === | ||
| + | Приведенный алгоритм можно записать с помощью псевдокода: | ||
| + | '''for''' <tex> i \leftarrow 1 </tex> '''to''' <tex> n </tex> '''do''' | ||
| + | '''for''' <tex> j \leftarrow 1 </tex> '''to''' <tex> i </tex> '''do''' | ||
| + | insert(<tex>s_{j..i}</tex>) | ||
| + | Поскольку операция insert может занимать линейное время, очевидно, что время работы данного алгоритма составляет <tex>O(n^3)</tex>. | ||
| + | |||
| + | == Возможные исходы операции insert == | ||
| + | Ниже приведены три возможных случая, которые могут возникнуть при добавлении подстроки <tex>s_{j..i}</tex> в дерево. | ||
| + | {| border="1" cellpadding="5" cellspacing="0" style="text-align:center" width=90% | ||
| + | !style="background:#f2f2f2"|Случай | ||
| + | !style="background:#f2f2f2"|Описание | ||
| + | !style="background:#f2f2f2"|Пример | ||
| + | |- | ||
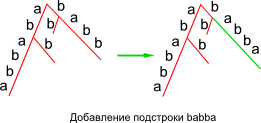
| + | |style="background:#ffffff"|''1. Продление листа'' | ||
| + | |style="background:#ffffff"|Пусть подстрока <tex>s_{j..i-1}</tex> кончается в листе. Добавим элемент <tex>s_i</tex> в конец последнего ребра. | ||
| + | |style="background:#ffffff"|[[Файл:Case2.png]] | ||
| + | |- | ||
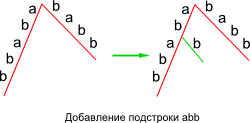
| + | |style="background:#ffffff"|''2. Создание листа'' | ||
| + | |style="background:#ffffff"|Пусть подстрока <tex>s_{j..i-1}</tex> кончается в вершине, не являющейся листом, из которой нет пути по символу <tex>s_i</tex>. Создадим новую дугу с началом в элементе <tex>s_{i-1}</tex> и листом <tex>s_i</tex>. | ||
| + | |style="background:#ffffff"|[[Файл:Case1.png]] | ||
| + | |- | ||
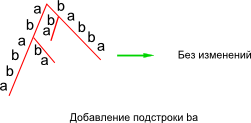
| + | |style="background:#ffffff"|''3. Ничего не делать'' | ||
| + | |style="background:#ffffff"|Пусть подстрока <tex>s_{j..i-1}</tex> кончается в вершине, из которой есть путь по <tex>s_i</tex>. Тогда ничего делать не надо. | ||
| + | |style="background:#ffffff"|[[Файл:Case3.png]] | ||
| + | |} | ||
| + | |||
| + | |||
==Оптимизация алгоритма Укконена== | ==Оптимизация алгоритма Укконена== | ||
{{Определение | {{Определение | ||
|definition= Пусть <tex>x\alpha</tex> обозначает произвольную строку, где <tex>x</tex> {{---}} ее первый символ, а <tex>\alpha</tex> {{---}} оставшаяся подстрока(возможно пустая). Если для внутренней вершины с путевой меткой <tex>x\alpha</tex> существует другая вершина <tex>s(v)</tex> с путевой меткой <tex>\alpha</tex> то ссылка из <tex>v</tex> в <tex>s(v)</tex> называется суффиксной ссылкой.}} | |definition= Пусть <tex>x\alpha</tex> обозначает произвольную строку, где <tex>x</tex> {{---}} ее первый символ, а <tex>\alpha</tex> {{---}} оставшаяся подстрока(возможно пустая). Если для внутренней вершины с путевой меткой <tex>x\alpha</tex> существует другая вершина <tex>s(v)</tex> с путевой меткой <tex>\alpha</tex> то ссылка из <tex>v</tex> в <tex>s(v)</tex> называется суффиксной ссылкой.}} | ||
| + | |||
| + | == Источник == | ||
| + | ''Дэн Гасфилд'' — '''Строки, деревья и последовательности в алгоритмах: Информатика и вычислительная биология''' — СПб.: Невский Диалект; БХВ-Петербург, 2003. — 654 с: ил. | ||
| + | |||
| + | [[Категория: Алгоритмы и структуры данных]] | ||
| + | [[Категория: Словарные структуры данных]] | ||
Версия 08:04, 20 марта 2011
Алгоритм Укконена — алгоритм построения суффиксного дерева для заданной строки за линейное время.
Содержание
Первая версия алгоритма
Рассмотрим сначала метод, который строит дерево за время , где — длина исходной строки . В дальнейшем данный алгоритм будет оптимизирован таким образом, что будет достигнута линейная скорость работы.
Описание
Алгоритм делится на фаз. В фазе с номером в дерево добавляются все суффиксы подстроки . При добавлении суффикса алгоритм сначала находит конец пути из корня, помеченного подстрокой , затем добавляет к концу этой подстроки очередной символ , если этот символ не был добавлен ранее.
Псевдокод
Приведенный алгоритм можно записать с помощью псевдокода:
for to do for to do insert()
Поскольку операция insert может занимать линейное время, очевидно, что время работы данного алгоритма составляет .
Возможные исходы операции insert
Ниже приведены три возможных случая, которые могут возникнуть при добавлении подстроки в дерево.
Оптимизация алгоритма Укконена
| Определение: |
| Пусть обозначает произвольную строку, где — ее первый символ, а — оставшаяся подстрока(возможно пустая). Если для внутренней вершины с путевой меткой существует другая вершина с путевой меткой то ссылка из в называется суффиксной ссылкой. |
Источник
Дэн Гасфилд — Строки, деревья и последовательности в алгоритмах: Информатика и вычислительная биология — СПб.: Невский Диалект; БХВ-Петербург, 2003. — 654 с: ил.