Алгоритм для причинно-согласованного порядка — различия между версиями
Yeputons (обсуждение | вклад) |
|||
| Строка 1: | Строка 1: | ||
| + | {| class="wikitable" align="center" style="color: red; background-color: black; font-size: 56px; width: 800px;" | ||
| + | |+ | ||
| + | |-align="center" | ||
| + | |'''НЕТ ВОЙНЕ''' | ||
| + | |-style="font-size: 16px;" | ||
| + | | | ||
| + | 24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. | ||
| + | |||
| + | Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. | ||
| + | |||
| + | Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. | ||
| + | |||
| + | Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. | ||
| + | |||
| + | ''Антивоенный комитет России'' | ||
| + | |-style="font-size: 16px;" | ||
| + | |Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению. | ||
| + | |-style="font-size: 16px;" | ||
| + | |[https://meduza.io/ meduza.io], [https://www.youtube.com/c/popularpolitics/videos Популярная политика], [https://novayagazeta.ru/ Новая газета], [https://zona.media/ zona.media], [https://www.youtube.com/c/MackNack/videos Майкл Наки]. | ||
| + | |} | ||
| + | |||
[[Категория: Параллельное программирование]] | [[Категория: Параллельное программирование]] | ||
Этот алгоритм берёт систему с асинхронным порядком и начинает гарантировать в ней [[Иерархия порядков сообщений#Причинно-согласованный порядок|причинно-согласованный порядок]]. | Этот алгоритм берёт систему с асинхронным порядком и начинает гарантировать в ней [[Иерархия порядков сообщений#Причинно-согласованный порядок|причинно-согласованный порядок]]. | ||
Версия 08:31, 1 сентября 2022
| НЕТ ВОЙНЕ |
|
24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России |
| Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению. |
| meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки. |
Этот алгоритм берёт систему с асинхронным порядком и начинает гарантировать в ней причинно-согласованный порядок.
Идея похожа на Алгоритм для FIFO порядка: прикрепить к каждому сообщению "номер" и обрабатывать только сообщения со следующим ожидаемым номером, а остальные складывать в очередь. Нам надо не только знать следующее ожидаемое сообщение от каждого процесса, но и
Используется что-то вроде матричных часов, но не совсем они (см. раздел 7.7 на странице 125 и раздел 12.2 на странице 193 в Gaarg).
Каждый процесс поддерживает счётчик-матрицу: $M_{i,j}$ — количество сообщений, отправленных процессом $i$ процессом $j$ (по мнению хранящего матрицу). Эта матрица отправляется с каждым сообщением, перед посылкой мы увеличиваем соответствующее число в ней на единицу.
Когда процесс $P_i$ с матрицей $M$ получил от $P_j$ сообщение с матрицей $W$, то:
- Если $W_{ji}=M_{ji}+1$, то это ожидаемое сообщение с точки зрения FIFO-порядка между $P_i$ и $P_j$. Иначе надо отложить в очередь.
- Если существует $k \neq j$ такое, что $W_{ki} > M_{ki}$, то это значит, что процесс $k$ отправил нам сообщение, процесс $j$ про это в курсе, а мы ещё его не получили. Тогда для причинно-согласованности надо сначала подождать это сообщение, а потом обрабатывать сообщение от $P_j$.
- Если же такого $k$ не существует, то уже можно обработать сообщение и ничего не нарушится (строго не доказывали).
- Непосредственно перед тем, как обработать сообщение, надо обновить свою матрицу $M$, взяв покомпонентный максимум всех значений.
Как и в алгоритме для FIFO, тут очередь принятых, но не обработанных сообщений может раздуваться бесконечно. Но тут нам сложнее обрабатывать сообщения в очереди: в FIFO это было независимо по процессам и можно было сложить их в очередь с приоритетом, а тут сообщение от одного процесса может вызвать лавину сообщений от остальных, надо перебирать.
Псевдокод
var
M:array[l..N, 1..N] of integer initially 0;
To send a message to :
M [i,j] := M[i,j] + 1;
send M as part of the message;
To receive a message with matrix W from Pj:
enabled if W[j,i] = M [j,i] + 1
M := max(M, W)
Пример
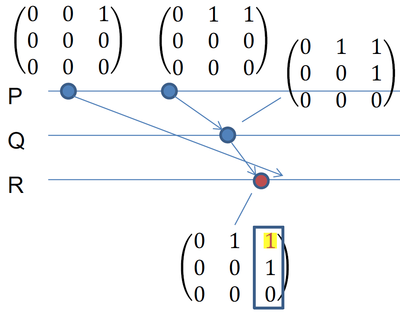
Пусть есть три процесса: $P$, $Q$, $R$ (пронумерованных так же) и они отправили друг другу сообщения. Процесс $R$ только что получил сообщение:
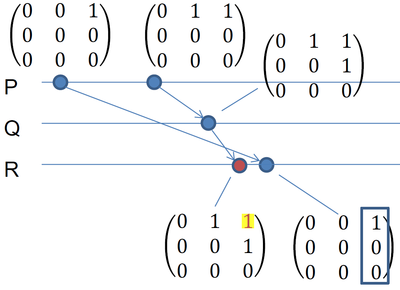
Так как у процесса $R$ матрица $M$ нулевая, а $W_{23}=1$, то FIFO-порядок не нарушен. Однако в столбце 3 (сообщения, посланные процессу $R$) в строчке 1 (от процесса $P$) есть единица, что больше, чем ноль. То есть $P$ послал сообщение $R$, $Q$ про это знает, но $R$ ещё это сообщение не получил. Тогда надо ждать сообщения, матрицу пока не обновляем.
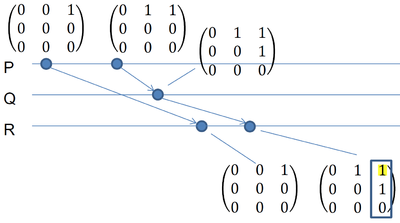
Тут как раз получили это сообщение. Столбец 3 совпадает, а в строчке 1 у нас на единицу больше, т.е. FIFO между $P$ и $Q$ не нарушен. Можно обработать сообщение и обновить матрицу $M$. Теперь можно обработать то сообщение, которое было получено первым: