|
|
| Строка 1: |
Строка 1: |
| − | {| class="wikitable" align="center" style="color: red; background-color: black; font-size: 56px; width: 800px;"
| |
| − | |+
| |
| − | |-align="center"
| |
| − | |'''НЕТ ВОЙНЕ'''
| |
| − | |-style="font-size: 16px;"
| |
| − | |
| |
| − | 24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян.
| |
| − |
| |
| − | Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием.
| |
| − |
| |
| − | Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей.
| |
| − |
| |
| − | Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить.
| |
| − |
| |
| − | ''Антивоенный комитет России''
| |
| − | |-style="font-size: 16px;"
| |
| − | |Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.
| |
| − | |-style="font-size: 16px;"
| |
| − | |[https://meduza.io/ meduza.io], [https://www.youtube.com/c/popularpolitics/videos Популярная политика], [https://novayagazeta.ru/ Новая газета], [https://zona.media/ zona.media], [https://www.youtube.com/c/MackNack/videos Майкл Наки].
| |
| − | |}
| |
| − |
| |
| | == Формулировка == | | == Формулировка == |
| | Пусть треугольник задан двумя векторам <tex>\overrightarrow{AB}</tex> и <tex>\overrightarrow{AC}</tex>. Необходимо найти центр и радиус вписанной окружности | | Пусть треугольник задан двумя векторам <tex>\overrightarrow{AB}</tex> и <tex>\overrightarrow{AC}</tex>. Необходимо найти центр и радиус вписанной окружности |
Текущая версия на 19:05, 4 сентября 2022
Формулировка
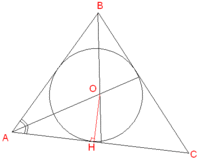
Пусть треугольник задан двумя векторам [math]\overrightarrow{AB}[/math] и [math]\overrightarrow{AC}[/math]. Необходимо найти центр и радиус вписанной окружности
Решение
Сначала найдем радиус окружности. Площадь треугольника [math]ABC[/math] мы можем найти из векторного произведения векторов [math]\overrightarrow{AB}[/math] и [math]\overrightarrow{AC}[/math]. С другой стороны, [math]S_{ABC} = S_{AOB} + S_{AOC} + S_{BOC}[/math]. А площадь маленьких треугольников равна половине произведения радиуса окружности на основание. Например, [math]S_{AOC} = \frac{1}{2} * R * AC[/math]. Отсюда получаем выражение, из которого можно найти радиус окружности. [math]R = \frac{|[\overrightarrow{AB} \times \overrightarrow{AC}]|}{AB + BC + AC}[/math]
Теперь будем искать центр окружности. Как известно, центр вписанной окружности лежит на пересечении биссектрис. Вектор, коллиниарный вектору [math]\overrightarrow{AO}[/math], можно найти следующим образом [math]\overrightarrow{l} = \frac{\overrightarrow{AB}}{AB} + \frac{\overrightarrow{AC}}{AC}[/math]. Обозначим вектор [math]\overrightarrow{l_1} = \frac{\overrightarrow{l}}{|\overrightarrow{l}|} [/math]. Теперь необходимо найти длину вектора [math]\overrightarrow{AO}[/math]. [math] AO = \frac{OH}{sin\frac{\alpha}{2}}[/math], где [math]\alpha = \angle{BAC}[/math]. По формуле понижения степени [math] sin^{2}\frac{\alpha}{2} = \frac{1 - cos\alpha}{2}[/math]. Найти [math]cos\alpha[/math] можно из скалярного произведения. [math]cos\alpha = \frac{(\overrightarrow{AB};\overrightarrow{AC})}{|\overrightarrow{AB}||\overrightarrow{AC}|}[/math]. Заметим, что [math]OH = R[/math], и можем выразить длину [math]AO = \frac{|[\overrightarrow{AB} \times \overrightarrow{AC}]|}{AB + BC + AC}\frac{\sqrt{2}|\overrightarrow{AB}||\overrightarrow{AC}|}{|\overrightarrow{AB}||\overrightarrow{AC}| - (\overrightarrow{AB};\overrightarrow{AC})}[/math]. Задача почти решена, осталось только отметить, что [math]AB = |\overrightarrow{AB}|, AC = |\overrightarrow{AC}|, BC = |\overrightarrow{AB} - \overrightarrow{AC}|[/math], а радиус-вектор точки центра окружности совпадает с радиус-вектором [math]\overrightarrow{AO} [/math], a [math]\overrightarrow{AO} = \overrightarrow{l_1} * AO [/math]