Алгоритм Фарака-Колтона и Бендера — различия между версиями
Kirelagin (обсуждение | вклад) (Текст, кажется, готов) |
Kirelagin (обсуждение | вклад) (Добавлена картинка) |
||
| Строка 5: | Строка 5: | ||
== Алгоритм == | == Алгоритм == | ||
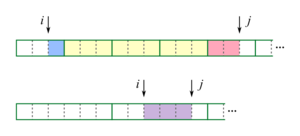
| + | [[Файл:F-C_B_algo.png|right|thumb|Части, из которых состоит ответ на запрос RMQ]] | ||
| + | |||
Данный алгоритм основывается на методе решения задачи RMQ с помощью [[Решение RMQ с помощью разреженной таблицы|разреженной таблицы (sparse table, ST)]] за <tex><O(N \log N),O(1)></tex>. | Данный алгоритм основывается на методе решения задачи RMQ с помощью [[Решение RMQ с помощью разреженной таблицы|разреженной таблицы (sparse table, ST)]] за <tex><O(N \log N),O(1)></tex>. | ||
Чтобы избавиться от логарифма используется предподсчёт ответа для небольших подстрок входной последовательности. Разделим последовательность <tex>a_i</tex> на блоки длины <tex>\frac{\log_2 N}{2}</tex>. Для каждого блока вычислим минимум на нём и определим <tex>b_i</tex> как позицию минимального элемента в <tex>i</tex>-том блоке. | Чтобы избавиться от логарифма используется предподсчёт ответа для небольших подстрок входной последовательности. Разделим последовательность <tex>a_i</tex> на блоки длины <tex>\frac{\log_2 N}{2}</tex>. Для каждого блока вычислим минимум на нём и определим <tex>b_i</tex> как позицию минимального элемента в <tex>i</tex>-том блоке. | ||
| − | На новой последовательности <tex>b_i</tex> построим [[Решение RMQ с помощью разреженной таблицы|разреженную таблицу]]. Теперь для ответа на запрос RMQ<tex>[i:j]</tex> нам необходимо вычислить следующее: | + | На новой последовательности <tex>b_i</tex> построим [[Решение RMQ с помощью разреженной таблицы|разреженную таблицу]]. Теперь для ответа на запрос RMQ<tex>[i:j]</tex>, если <tex>i</tex> и <tex>j</tex> находятся в разных блоках, нам необходимо вычислить следующее: |
# Минимум на отрезке от <tex>i</tex> до конца содержащего <tex>i</tex> блока. | # Минимум на отрезке от <tex>i</tex> до конца содержащего <tex>i</tex> блока. | ||
# Минимум по всем блокам, находящимся между блоками, содержащими <tex>i</tex> и <tex>j</tex>. | # Минимум по всем блокам, находящимся между блоками, содержащими <tex>i</tex> и <tex>j</tex>. | ||
| Строка 16: | Строка 18: | ||
Второй элемент мы уже умеем находить за <tex>O(1)</tex> с помощью <tex>b_i</tex> и ST. Осталось научиться находить минимум по отрезку, границы которого не совпадают с границами блоков. | Второй элемент мы уже умеем находить за <tex>O(1)</tex> с помощью <tex>b_i</tex> и ST. Осталось научиться находить минимум по отрезку, границы которого не совпадают с границами блоков. | ||
| + | |||
| + | === Минимум внутри блока === | ||
{{Утверждение | {{Утверждение | ||
Версия 22:40, 9 мая 2011
Алгоритм Фарака-Колтона, Бендера (алгоритм Фарах-Колтона, Бендера) — применяется для решения специального случая задачи RMQ (поиск минимума на отрезке), в котором соседние элементы входной последовательности различаются на ±1 за времени. Может быть использован также для решения задачи LCA.
Вход: последовательность длины .
Выход: ответы на онлайн запросы вида «минимум на отрезке ».
Алгоритм
Данный алгоритм основывается на методе решения задачи RMQ с помощью разреженной таблицы (sparse table, ST) за .
Чтобы избавиться от логарифма используется предподсчёт ответа для небольших подстрок входной последовательности. Разделим последовательность на блоки длины . Для каждого блока вычислим минимум на нём и определим как позицию минимального элемента в -том блоке.
На новой последовательности построим разреженную таблицу. Теперь для ответа на запрос RMQ, если и находятся в разных блоках, нам необходимо вычислить следующее:
- Минимум на отрезке от до конца содержащего блока.
- Минимум по всем блокам, находящимся между блоками, содержащими и .
- Минимум от начала блока, содержащего , до .
Ответом на запрос будет позиция меньшего из эти трёх элементов.
Второй элемент мы уже умеем находить за с помощью и ST. Осталось научиться находить минимум по отрезку, границы которого не совпадают с границами блоков.
Минимум внутри блока
| Утверждение: |
Если две последовательности и таковы, что все их элементы на соответствующих позициях различаются на одну и ту же константу (т.е. ), то любой запрос RMQ даст один и тот же ответ для обеих последовательностей. |
Таким образом, мы может нормализовать блок, вычтя из всех его элементов первый. Тем самым мы значительно уменьшим число возможных типов блоков.
| Утверждение: |
Существует различных типов нормализованных блоков. |
| Соседние элементы в блоках отичаются на ±1. Первый элемент в нормализованном блоке всегда равен нулю. Таким образом, каждый нормализованный блок может быть представлен ±1-вектором длины . Таких векторов . |
Осталось создать таблиц — по одной для каждого типа блока. В такую таблицу необходимо занести предподсчитанные ответы на все возможные запросы, коих . Таким образом мы получили возможность отвечать на запрос минимума по любой части блока за , затратив на предподсчёт времени. Для каждого блока в необходимо заранее вычислить его тип.
Результат
Итого, на предподсчёт требуется времени и памяти, а ответ на запрос вычисляется за .
См. также
- Решение RMQ с помощью разреженной таблицы
- Сведение задачи RMQ к задаче LCA
- Сведение задачи LCA к задаче RMQ
Ссылки
- M. A. Bender and M. Farach-Colton. “The LCA Problem Revisited” LATIN, pages 88-94, 2000