Примеры неразрешимых задач: задача о замощении

Определения

Определение: Полимино (англ. polyomino) — плоская геометрическая фигура, состоящая из [math]n[/math] одноклеточных квадратов, соединенных по сторонам.

Определение:

Замощение плоскости (англ. tiling) — представление плоскости в виде множества непересекающихся полимино.

Пусть дана плоскость [math]S[/math] и набор полимино [math]P[/math], если [math]\exists ~ f: N \times N \to P[/math] (говорящая по клетке, какому полимино она соответствует) тогда считается, что можно замостить плоскость [math]S[/math] данным набором.

Замощение четверти плоскости

Задача:

Пусть даны некоторые типы полимино, причем экземпляров каждого типа дается бесконечно много. Верно ли, что используя любое количество полимино можно полностью замостить без пропусков и выступов четверть плоскости? Поворачивать полимино не разрешено.

Теорема:

Задача о замощении четверти плоскости полимино неразрешима.

Доказательство:

[math]\triangleright[/math]

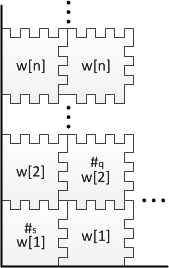
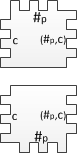
Сведём задачу останова к данной задаче. Пусть дана машина Тьюринга [math]M =\langle \Sigma, Q, \Pi, B \in \Pi, s,\delta: Q \times \Pi \rightarrow Q \times \Pi \times \{ \leftarrow, \downarrow, \rightarrow \} \rangle[/math] и слово [math]w \in \Sigma^*[/math]. Требуется определить, остановится ли данная МТ на входе [math]w[/math]. Для того, чтобы доказать неразрешимость задачи о замощении, для заданной машины Тьюринга [math]M[/math] и слова [math]w[/math] построим набор полимино, которым можно замостить четверть плоскости, если МТ не остановится на заданном слове. Если же МТ останавливается, то четверть плоскости полученным набором замостить невозможно. Будем эмулировать процесс выполнения МТ на входе [math]w \in \Sigma^*[/math] путем построения вертикальных рядов, каждый из которых эквивалентен конфигурации МТ на определенном этапе выполнения. Первый ряд эквивалентен начальной конфигурации МТ, а каждый следующий ряд соответствует следующей конфигурации. Говоря простым языком, каждый ряд представляет из себя "снимок" состояния машины на соответствующем этапе выполнения. На рисунке сверху изображены два вертикальных ряда полимино. Первый ряд соответствует МТ и слову [math]w[/math]. Первое полимино соответствует паре из первого символа и начального состояния, все остальные — символам из [math]w[/math]. Во втором ряду второе полимино соответствует паре из символа [math]w[2][/math] и состояния [math]q[/math]. То есть МТ сделала переход [math]\delta (s, w[1]) = \langle q, w[1], \rightarrow \rangle[/math]. Теперь на основе заданной МТ будем строить набор полимино, которые будут иметь следующий вид: На каждой стороне такого полимино находится определенное число выступов/впадин. Каждому символу из алфавита, состоянию и паре из состояния и символа сопоставим некоторое уникальное число (можно ограничить [math]k \leqslant |\Pi| + |Q| + |\Pi \times Q| + 1[/math]) – это и будет количество выступов/впадин, находящихся на одной стороне полимино. 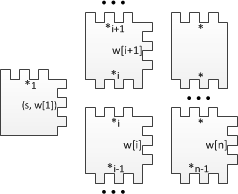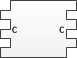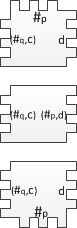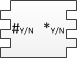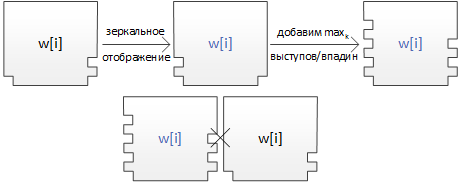Сначала построим набор полимино, который задаёт начальную конфигурацию: где [math]*i[/math] – уникальное число для каждой смежной пары полимино из начальной конфигурации. Первое полимино характеризует начальное состояние, последующие за ним кодируют входное слово, и завершающее полимино требуется для корректного замощения оставшейся части ряда. Далее строим полимино для всех элементов алфавита [math]c \in \Pi[/math]: В нем количество впадин слева равно количеству выступов справа. Такой тип полимино передает содержимое ленты МТ следующему ряду. Теперь построим полимино для функции перехода [math]\delta (q, c) = \langle p, d, D \rangle [/math], где [math]q \in Q, p \in Q, c \in \Pi, d \in \Pi, D\in \{\leftarrow, \downarrow, \rightarrow \}[/math]: На рисунке изображены (снизу вверх) полимино соответствующие значениям [math]D = \{\leftarrow, \downarrow, \rightarrow \}[/math]. Вместе со следующим типом они эмулируют перемещение головки МТ. Далее построим следующий тип полимино: Эти полимино получают на вход символ алфавита [math]c[/math] от предыдущего ряда и состояние [math]p[/math] от соседнего полимино, а затем передает следующему ряду пару из состояния и символа. Построим последний тип полимино, характеризующих состояния [math]\#_Y[/math] и [math]\#_N[/math]: Такое полимино имеет уникальное число выступов справа. Ни одно другое полимино из полученного набора не сможет к нему присоединиться, и процесс дальнейшего замощения будет невозможен. Полученный алгоритм сведения получает на вход МТ и слово, а на выход выдает соответствующий им набор полимино. Таким образом, четверть плоскости можно замостить тогда и только тогда, когда закодированная МТ не останавливается на данном входе. Иными словами, есть бесконечное количество конфигураций, не переходящих в конечное состояние. Это значит, что мы сможем замощать плоскость ряд за рядом бесконечное количество раз, что в результате замостит плоскость. Если же МТ остановится, то и замостить четверть плоскости мы не сможем из-за того, что конечное полимино не имеет продолжения. Значит задача о замощении полимино не разрешима.

[math]\triangleleft[/math]

Замощение половины плоскости

Теорема:

Задача о замощении половины плоскости полимино неразрешима.

Доказательство:

[math]\triangleright[/math]

Будем действовать также как и предыдущем доказательстве, только одновременно будем строить еще и зеркально отраженные полимино так, чтобы их нельзя было никак соединить с изначальными. Например, можно сделать новое количество выступов/впадин [math]k' = \mathrm{cur_k} + \mathrm{max_k}[/math], где [math]\mathrm{cur_k}[/math] — количество выступов/впадин у полимино, от которого образовалось текущее, [math]\mathrm{max_k}[/math] — максимальное число выступов/впадин у полимино в первой четверти. Сделаем так для всех полимино кроме первого столбца. Для него добавим специальное соединение, к которому подходит только зеркально отраженное полимино.

[math]\triangleleft[/math]

Замощение целой плоскости

Теорема:

Задача о замощении целой плоскости полимино неразрешима.

Доказательство:

[math]\triangleright[/math]

Аналогично замощению половины плоскости.

[math]\triangleleft[/math]

См. также

• Задача о выводе в полусистеме Туэ
• Проблема соответствий Поста
• M-сводимость
• Неразрешимость исчисления предикатов первого порядка

Источники информации

• Полимино — Википедия
• The tiling problem
• The domino problem