Реализация запроса в дереве отрезков снизу — различия между версиями
Gemin (обсуждение | вклад) (→Алгоритм) |
(→Алгоритм) |
||
| Строка 4: | Строка 4: | ||
[[Файл:Down-up1.png|right|350px|thumb|Реализация запроса снизу вверх]] | [[Файл:Down-up1.png|right|350px|thumb|Реализация запроса снизу вверх]] | ||
Будем рассматривать дерево отрезков с операцией нахождения минимального значения на отрезке(RMQ).<br> | Будем рассматривать дерево отрезков с операцией нахождения минимального значения на отрезке(RMQ).<br> | ||
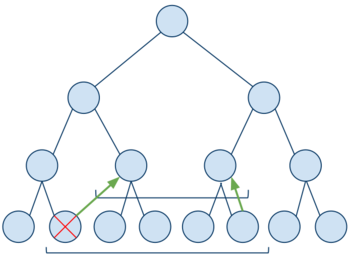
| − | Установим границы отрезка на соответствующие листья. Если элемент попавший на левую границу является правым сыном, то отрезаем его | + | Установим границы отрезка на соответствующие листья. Если элемент попавший на левую границу является правым сыном, то отрезаем его, левая граница перемещается на один элемент вправо; в другом случае левую границу не трогаем. Аналогично рассматриваем элемент попавший на правую границу (является ли этот элемент левым сыном). Затем устанавливаем границы отрезка на родительские элементы текущих границ. Отрезая элемент, мы считаем минимум из отрезанного и минимума на оставшемся отрезке. Закончим алгоритм, когда границы пересекутся. |
==Псевдокод== | ==Псевдокод== | ||
Версия 23:02, 17 мая 2011
Содержание
Описание
Реализация запроса снизу вверх в дереве отрезков является, в отличие от реализации сверху вниз, итеративным методом.
Алгоритм
Будем рассматривать дерево отрезков с операцией нахождения минимального значения на отрезке(RMQ).
Установим границы отрезка на соответствующие листья. Если элемент попавший на левую границу является правым сыном, то отрезаем его, левая граница перемещается на один элемент вправо; в другом случае левую границу не трогаем. Аналогично рассматриваем элемент попавший на правую границу (является ли этот элемент левым сыном). Затем устанавливаем границы отрезка на родительские элементы текущих границ. Отрезая элемент, мы считаем минимум из отрезанного и минимума на оставшемся отрезке. Закончим алгоритм, когда границы пересекутся.
Псевдокод
Псевдокод функции нахождения минимума на отрезке .
segmentMin(left, right)
res = MAX_INT;
while left < right
if left == <правый сын>
res = min(result, data[left]);
left = parent(left + 1);
else
left = parent(left);
if right == <левый сын>
result = min(result, data[right]);
right = parent(right - 1);
else
right = parent(right);
if left == right
result = min(result, data[left]);
return result;
Функция возвращает родителя аргумента.