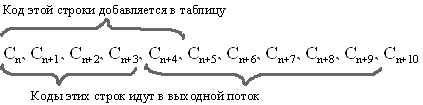Алгоритм LZW
| Определение: |
| Алгори́тм Ле́мпеля — Зи́ва — Ве́лча (Lempel-Ziv-Welch, LZW) — это универсальный алгоритм сжатия данных без потерь |
Непосредственным предшественником LZW явился алгоритм LZ78, опубликованный Абрахамом Лемпелем(Abraham Lempel) и Якобом Зивом (Jacob Ziv) в 1978 г. Этот алгоритм воспринимался как математическая абстракция до 1984 г., когда Терри Уэлч (Terry A. Welch) опубликовал свою работу с модифицированным алгоритмом, получившим в дальнейшем название LZW (Lempel-Ziv-Welch).
Содержание
Применение
Опубликование алгоритма LZW произвело большое впечатление на всех специалистов по сжатию информации. За этим последовало большое количество программ и приложений с различными вариантами этого метода.
Этот метод позволяет достичь одну из наилучших степеней сжатия среди других существующих методов сжатия графических данных, при полном отсутствии потерь или искажений в исходных файлах. В настоящее время испольуется в файлах формата TIFF, PDF, GIF, PostScript и других, а также отчасти во многих популярных программах сжатия данных (ZIP, ARJ, LHA).
Описание
Процесс сжатия выглядит следующим образом. Последовательно считываются символы входного потока и происходит проверка, существует ли в созданной таблице строк такая строка. Если такая строка существует, считывается следующий символ, а если строка не существует, в поток заносится код для предыдущей найденной строки, строка заносится в таблицу, а поиск начинается снова.
Например, если сжимают байтовые данные (текст), то строк в таблице окажется 256 (от "0" до "255"). Если используется 10-битный код, то под коды для строк остаются значения в диапазоне от 256 до 1023. Новые строки формируют таблицу последовательно, т. е. можно считать индекс строки ее кодом.
Алгоритму декодирования на входе требуется только закодированный текст, поскольку он может воссоздать соответствующую таблицу преобразования непосредственно по закодированному тексту.
Алгоритм
- Инициализация словаря всеми возможными односимвольными фразами. Инициализация входной фразы ω первым символом сообщения.
- Считать очередной символ K из кодируемого сообщения.
- Если КОНЕЦ_СООБЩЕНИЯ, то выдать код для ω, иначе
- Если фраза ωK уже есть в словаре, присвоить входной фразе значение ωK и перейти к Шагу 2, иначе выдать код ω, добавить ωK в словарь, присвоить входной фразе значение K и перейти к Шагу 2.
Конец
Пример
Рассмотрим пример сжатия и декодирования изображения.
Сначала создадим начальный словарь единичных символов. В стандартной кодировке ASCII имеется 256 различных символов, поэтому, для того, чтобы все они были корректно закодированы (если нам неизвестно, какие символы будут присутствовать в исходном файле, а какие - нет), начальный размер кода будет равен 8 битам. Если нам заранее известно, что в исходном файле будет меньшее количество различных символов, то вполне разумно уменьшить количество бит. Чтобы инициализировать таблицу, мы установим соответствие кода 0 соответствующему символу с битовым кодом 00000000, тогда 1 соответствует символу с кодом 00000001, и т.д., до кода 255. На самом деле мы указали, что каждый код от 0 до 255 является корневым.
| Символ | Битовый код |
|---|---|
| a | 000 |
| b | 001 |
| c | 010 |
| d | 011 |
| e | 100 |
Больше в таблице не будет других кодов, обладающих этим свойством.
По мере роста словаря, размер групп должен расти, с тем, чтобы учесть новые элементы. 8-битные группы дают 256 возможных комбинации бит, поэтому, когда в словаре появится 256-е слово, алгоритм должен перейти к 9-битным группам. При появлении 512-ого слова произойдет переход к 10-битным группам, что дает возможность запоминать уже 1024 слова и т.д.
В нашем примере алгоритму заранее известно о том, что будет использоваться всего 5 различных символов, следовательно, для их хранения будет использоваться минимальное количество бит, позволяющее нам их запомнить, то есть 3 ( 8 различных комбинаций ).
Кодирование
Пусть мы сжимаем последовательность "abacabadabacabae".
Тогда, согласно изложенному выше алгоритму, мы добавим к изначально пустой строке “a” и проверим, есть ли строка “a” в таблице. Поскольку мы при инициализации занесли в таблицу все строки из одного символа, то строка “a” есть в таблице. Далее мы читаем следующий символ "b" из входного потока и проверяем, есть ли строка “ab” в таблице. Такой строки в таблице пока нет. Добавляем в таблицу <5> “ab”. В поток: <0>; “ba” — нет. В таблицу: <6> “ba”. В поток: <1>; “ac” — нет. В таблицу: <7> “ac”. В поток: <0>; “ca” — нет. В таблицу: <8> “ca”. В поток: <2>; “ab” — есть в таблице; “aba” — нет. В таблицу: <9> “aba”. В поток: <5>; “ad” — нет. В таблицу: <10> “ad”. В поток: <0>; “da” — нет. В таблицу: <11> “da”. В поток: <3>; “aba” — есть в таблице; “abac” — нет. В таблицу: <12> “abac”. В поток: <9>; “ca” — есть в таблице; “cab” — нет. В таблицу: <13> “cab”. В поток: <8>; “ba” — есть в таблице; “bae” — нет. В таблицу: <14> “bae”. В поток: <6>; И, наконец последняя строка “e”, за ней идет конец сообщения, поэтому мы просто выводим в поток <4>.
| Текущий символ | Следующий символ | Вывод | Словарь | ||
|---|---|---|---|---|---|
| Код | Биты | ||||
| a | b | 0 | 000 | 5: | ab |
| b | a | 1 | 001 | 6: | ba |
| a | c | 0 | 000 | 7: | ac |
| c | a | 2 | 010 | 8: | ca |
| a | b | - | - | - | - |
| b | a | 5 | 101 | 9: | aba |
| a | d | 0 | 000 | 10: | ad |
| d | a | 3 | 011 | 11: | da |
| a | b | - | - | - | - |
| b | a | - | - | - | - |
| a | c | 9 | 1001 | 12: | abac |
| c | a | - | - | - | - |
| a | b | 8 | 1000 | 13: | cab |
| b | a | - | - | - | - |
| a | e | 6 | 0110 | 14: | bae |
| e | - | 4 | 0100 | - | - |
Итак, мы получаем закодированное сообщение "0 1 0 2 5 0 3 9 8 6 4", что на 11 бит короче.
Декодирование
Особенность LZW заключается в том, что для декомпрессии нам не надо сохранять таблицу строк в файл для распаковки. Алгоритм построен таким образом, что мы в состоянии восстановить таблицу строк, пользуясь только потоком кодов.
Теперь представим ,что мы получили закодированное сообщение, приведённое выше, и нам нужно его декодировать. Прежде всего, нам нужно знать начальный словарь, а последующие записи словаря мы можем реконструировать уже на ходу, поскольку они являются просто конкатенацией предыдущих записей.
| Данные | На выходе | Новая запись | ||||
|---|---|---|---|---|---|---|
| Биты | Код | Полная | Частичная | |||
| 000 | 0 | a | - | - | 5: | a? |
| 001 | 1 | b | 5: | ab | 6: | b? |
| 000 | 0 | a | 6: | ba | 7: | a? |
| 010 | 2 | c | 7: | ac | 8: | c? |
| 101 | 5 | ab | 8: | ca | 9: | ab? |
| 000 | 0 | a | 9: | aba | 10: | a? |
| 011 | 3 | d | 10: | ad | 11: | d? |
| 1001 | 9 | aba | 11: | da | 12: | aba? |
| 1000 | 8 | ca | 12: | abac | 13: | c? |
| 0110 | 6 | ba | 13: | cab | 14: | ba? |
| 0100 | 4 | e | 14: | bae | - | - |
Примечание
Для повышения степени сжатия изображений данным методом часто используется одна «хитрость» реализации этого алгоритма. Некоторые файлы, подвергаемые сжатию с помощью LZW, имеют часто встречающиеся цепочки одинаковых символов, например aaaaaa … или 30, 30, 30 … и т. п. Их непосредственное сжатие будет генерировать выходной код 0, 0, 5 и т.д. Спрашивается, можно ли в этом частном случае повысить степень сжатия?
Оказывается, это возможно, если оговорить некоторые действия:
Мы знаем, что для каждого кода надо добавлять в таблицу строку, состоящую из уже присутствующей там строки и символа, с которого начинается следующая строка в потоке.
Итак, кодер заносит первую «а» в строку, ищет и находит "а" в словаре. Добавляет в строку следующую "а", находит, что "аа" нет в словаре. Тогда он добавляет запись <5>: "аа" в словарь и выводит метку <0> ("а") в выходной поток. Далее строка инициализируется второй «а», то есть принимает вид "a?" вводится третья «а», строка вновь равна "аа", которая теперь имеется в словаре. Если появляется четвертая «а», то строка "aa?" равна "ааа", которой нет в словаре. Словарь пополняется этой строкой, а на выход идет метка <5> ("aa"). После этого строка инициализируется третьей «а», и т.д. и т.п. Дальнейший процесс вполне ясен.
В результате на выходе получаем последовательность 0, 5, 6 …, которая короче прямого кодирования стандартным методом LZW.
Можно показать, что такая последовательность будет корректно восстановлена. Декодировщик сначала читает первый код – это <0>, которому соответствует символ "a". Затем читает код <5>, но этого кода в его таблице нет. Но мы уже знаем, что такая ситуация возможна только в том случае, когда добавляемый символ равен первому символу только что считанной последовательности, то есть "a". Поэтому он добавит в свою таблицу строку "aa" с кодом <5>, а в выходной поток поместит "aa". И так может быть раскодирована вся цепочка кодов.
Мало того, описанное выше правило кодирования мы можем применять в общем случае не только к подряд идущим одинаковым символам, но и к последовательностям, у которых очередной добавляемый символ равен первому символу цепочки.
Достоинства и недостатки
+ Не требует вычисления вероятностей встречаемости символов или кодов. + Для декомпрессии не надо сохранять таблицу строк в файл для распаковки. Алгоритм построен таким образом, что мы в состоянии восстановить таблицу строк, пользуясь только потоком кодов. + Данный тип компрессии не вносит искажений в исходный графический файл, и подходит для сжатия растровых данных любого типа. - Алгоритм не проводит анализ входных данных поэтому не оптимален.
Патенты
На алгоритм LZW и его вариации был выдан ряд патентов, как в США, так и в других странах.
Среди обладателей патентов была компания Unisys. Поэтому использование формата GIF, в котором он используется, было раскритиковано из-за лицензионных отчислений. Был предложен альтернативный формат PNG (PNG not GIF).
Когда в 2003 году закончился срок действия патента на метод сжатия данных LZW, он остался востребованным только для формата GIF.