| Определение: |
| Недетерминированный конечный автомат (НКА) — это пятерка [math]\langle \Sigma , Q, s \in Q, T \subset Q, \delta : Q \times \Sigma \to 2^Q \rangle[/math], где [math]\Sigma[/math] — алфавит, [math]Q[/math] — множество состояний автомата, [math]s[/math] — начальное состояние автомата, [math]T[/math] — множество допускающих состояний автомата, [math]\delta[/math] — функция переходов.
Таким образом единственное отличие НКА от ДКА — это существование нескольких переходов по одному символу из одного состояния. |
Процесс допуска
| Определение: |
| Мгновенная кофигурация — это пара [math] \langle p, q \rangle [/math], [math] p \in Q [/math], [math] q \in \Sigma^*[/math] |
Определим некоторые операции для мгновенных конфигураций.
| Определение: |
Говорят, что [math] \langle p, \beta \rangle[/math] выводится за один шаг из [math]\langle q, \alpha \rangle [/math], если:
- [math]\alpha = c\beta[/math]
- [math]p \in \delta (q, c)[/math].
Это также записывают так: [math]\langle q, \alpha \rangle \vdash \langle p, \beta \rangle[/math] |
| Определение: |
Говорят, что [math] \langle p, \beta \rangle[/math] выводится за ноль и более шагов из [math]\langle q, \alpha \rangle [/math], если [math]\exists n[/math]:
- [math]\langle q, c_1 c_2 c_3 ...c_n\beta \rangle \vdash \langle u_1, c_2 c_3 ...c_n\beta \rangle \vdash \langle u_2, c_3 ...c_n\beta \rangle ...\vdash \langle u_{n-1}, c_n\beta \rangle \vdash \langle p, \beta \rangle[/math]
Это также записывают так: [math]\langle q, \alpha \rangle \vdash^* \langle p, \beta \rangle[/math] |
| Определение: |
| НКА допускает слово [math]\alpha[/math], если [math]\exists t \in T: \langle s, \alpha \rangle \vdash^* \langle t, \varepsilon \rangle[/math]. |
Менее формально это можно описать так: НКА допускает слово [math] \alpha [/math], если существует путь из начального состояния в какое-то терминальное, такое что буквы, выписанные с переходов на этом пути по порядку, образуют слово [math] \alpha [/math].
Язык автомата
| Определение: |
Множество слов, допускаемых автоматом [math] \mathcal{A} [/math], называется языком НКА [math] \mathcal{A} [/math].
- [math] \mathcal{L}(\mathcal{A}) = \lbrace w | \exists t \in T : \langle s, w \rangle \vdash^* \langle t, \varepsilon \rangle \rbrace [/math]
|
Язык НКА тоже является автоматным языком, так как можно построить из НКА эквивалентный ДКА, поэтому вычислительная мощность этих двух автоматов совпадает.
Пример
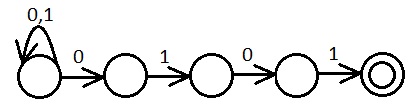
Автомат, допускающий слова над алфавитом из символов 0 и 1, допускающий слова оканчивающиеся на 0101.
(0|1)*0101
Алгоритм определяющий допустимость автоматом слова
По сравнению с ДКА, определять допускает ли НКА слово сложнее, так как из состояния теперь есть несколько переходов по букве и выбрать случайный переход нельзя.
Поступим по-другому, определим множество всех достижимых состояний из стартового по слову [math] \alpha [/math].
- [math] R(\alpha) = \lbrace p | \langle s, \alpha \rangle \vdash^* \langle p, \varepsilon \rangle \rbrace [/math]
Пусть нам нужно определить допускает ли НКА слово [math] w [/math]. Заметим, что если [math] \exists t \in T : t \in R(w) [/math], то слово допускается, так как [math] \langle s, w \rangle \vdash^* \langle t, \varepsilon \rangle [/math] по определению [math] R(w) [/math]. Алгоритм состоит в том, чтобы построить [math] R(w) [/math].
Очевидно, что [math] R(\varepsilon) = \lbrace s \rbrace [/math]. Пусть мы построили [math] R(\alpha) [/math], как же получить [math] R(\alpha c)[/math], где [math] c \in \Sigma [/math]. Заметим, что
- [math] R(\alpha c) = \lbrace q | q \in \delta(p, c), p \in R(\alpha) \rbrace [/math],
так как
- [math] \langle s, \alpha \rangle \vdash^* \langle p, \varepsilon \rangle \Rightarrow \langle s, \alpha c \rangle \vdash^* \langle p, c \rangle \vdash \langle q, \varepsilon \rangle \Rightarrow \langle s, \alpha c \rangle \vdash^* \langle q, \varepsilon \rangle [/math], где [math] q \in \delta(p, c) [/math]
Теперь, когда мы научились добавлять символ к строке, возьмем [math] R(\varepsilon) [/math], будем добавлять [math] w_1, w_2 \ldots w_{|w|} [/math] и находить для каждого [math] R(w_1\ldots w_k) [/math].
Когда мы получим [math] R(w) [/math], проверим что в нем есть терминальное состояние.
Псевдокод:
[math] R_0 = \lbrace s \rbrace [/math]
for i = 1 to length(w) do
[math] R_i = \varnothing [/math]
for [math] p \in R_{i - 1} [/math] do
[math] R_i = R_i \cup \delta(p, w_i) [/math]
accepts = False
for [math] t \in T [/math] do
if ([math] t \in R_{|w|} [/math]) then
accepts = True
См. также
