| Определение: |
Детерменированным автоматом с магазинной памятью называется автомат с магазинной памятью, для которого выполнены следующие условия:
- [math]\mathcal8 q \in Q, a \in \Sigma \cup \{ \varepsilon \}, X \in \Gamma \Rightarrow \delta(q, a, X)[/math] имеет не более одного элемента — [math] \delta : Q \times \Sigma \cup \{\varepsilon\} \times \Gamma \rightarrow Q \times \Gamma^*[/math].
- Если [math]\delta (q,a,X)[/math] непусто для некоторого [math]a \in \Sigma[/math], то [math]\delta (q,\epsilon,X)[/math] должно быть пустым.
|
Будем обозначать переход автомата из состояния [math](q_1,a_1,X_1)[/math] в состояние [math](q_2,a_2,X_2)[/math] как [math](q_1,a_1,X_1)\vdash(q_2,a_2,X_2)[/math]. Переход автомата из состояния [math](q_1,a_1,X_1)[/math] в состояние [math](q_{p+1},a_{p+1},X_{p+1})[/math] через [math]P[/math] промежуточных состояний обозначаем [math](q_1,a_1,X_1)\vdash^*_P(q_{p+1},a_{p+1},X_{p+1})[/math].
Пример
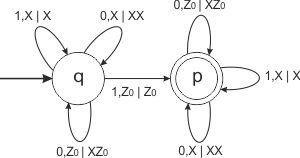
Автомат [math]A=(\{0,1\},\{q,p\},q, \{Z_0,X\}, Z_0,\{p\}, \delta)[/math] с функией перехода [math]\delta[/math]:
- [math]\delta(q,0,Z_0)=(q,XZ_0)[/math]
- [math]\delta(q,0,X)=(q,XX)[/math]
- [math]\delta(q,1,X)=(q,X)[/math]
- [math]\delta(q,1,Z_0)=(p,Z_0)[/math]
- [math]\delta(p,0,Z_0)=(p,XZ_0)[/math]
- [math]\delta(p,0,X)=(p,XX)[/math]
- [math]\delta(p,1,X)=(p,X)[/math]
Источники
- Хопкрофт Д., Мотвани Р., Ульман Д. Введение в теорию автоматов, языков и вычислений, 2-е изд.. : Пер. с англ. — М. : Издательский дом "Вильямс", 2002.
