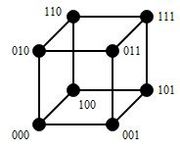
Расстояние Хэмминга
| Определение: |
| Расстояние Хэмминга (Hamming distance) — число позиций, в которых различаются соответствующие символы двух строк одинаковой длины. |
В более общем случае расстояние Хэмминга применяется для строк одинаковой длины любых k-ичных алфавитов и служит метрикой различия (функцией, определяющей расстояние в метрическом пространстве) объектов одинаковой размерности.
Пример
Свойства
Расстояние Хэмминга обладает свойствами метрики, так как удовлетворяет ее определению.
- (Если расстояние от до равно нулю, то и совпадают ())
- (Объект удален от объекта так же, как объект удален от объекта )
- (Расстояние от до всегда меньше или равно расстоянию от до через точку . Это свойство обычно называют неравенством треугольника за его естественную геометрическую аналогию: сумма двух сторон треугольника всегда больше третьей стороны.)
Доказательство неравенства треугольника
| Утверждение: |
|
Доказательство №1 Пусть слова и отличаются в некоторых позициях. Тогда какое бы слово мы ни взяли, оно будет отличаться в каждой из этих позиций по крайне мере от одного из слов и . Следовательно, суммируя в правой части и , мы обязательно учтем все позиции, в которых различались слова и . Т.е. получается, что .
I. Все позиции независимы. II. Рассмотрим два варианта, когда (1) и (2):
а) База индукции: Пусть слова и отличаются в некоторой позиции. Тогда какое бы слово мы не взяли оно будет отличатся хотя бы от одного из слов или . А это означает, что неравенство выполняется. б) Пусть неравенство выполняется при . Докажем, что оно верно для . Для позиций из общее количество отличий слова от и слова от , благодаря предположению , не меньше, чем количество отличий слова от . Рассмотрим оставшуюся позицию, в которой отличаются слова и . Так как какое бы слово мы не взяли оно, в этой позиции, будет отличатся хотя бы от одного из слов или , то неравенство для выполняется. Индуктивное предположение верно, значит, неравенство выполняется для любого натурального ( — количество отличий слова от ). |