Алгоритм Краскала

Алгоритм Краскала — алгоритм поиска минимального остовного дерева (minimum spanning tree, MST) во взвешенном неориентированном связном графе.

Идея

Будем последовательно строить подграф [math]F[/math] графа [math]G[/math] ("растущий лес"), поддерживая следующий инвариант: на каждом шаге [math]F[/math] можно достроить до некоторого MST. Начнем с того, что включим в [math]F[/math] все вершины графа [math]G[/math]. Теперь будем обходить множество [math]EG[/math] в порядке увеличения веса ребер. Добавление очередного ребра [math]e[/math] в [math]F[/math] может привести к возникновению цикла в одной из компонент связности [math]F[/math]. В этом случае, очевидно, [math]e[/math] не может быть включено в [math]F[/math]. В противном случае [math]e[/math] соединяет разные компоненты связности [math]F[/math], тогда существует разрез [math] \langle S, T \rangle [/math] такой, что одна из компонент связности составляет одну его часть, а оставшаяся часть графа - вторую. Тогда [math]e[/math] и есть минимальное ребро, пересекающее этот разрез. Значит, из леммы о безопасном ребре следует, что [math]F+e[/math] можно продолжить до MST, поэтому добавим это ребро в [math]F[/math].
Несложно понять, что после выполнения такой процедуры получится остовное дерево, при этом его минимальность вытекает из леммы о безопасном ребре.

Реализация

Вход: граф [math]G = (V, E)[/math]
Выход: минимальный остов [math]F[/math] графа [math]G[/math]
1) [math]F := (V, \varnothing)[/math]
1) Отсортируем [math]E[/math] по весу ребер.
2) Заведем систему непересекающихся множеств (DSU) и инициализируем ее множеством [math]V[/math].
3) Перебирая ребра [math]uv \in EG[/math] в порядке увеличения веса, смотрим, принадлежат ли [math]u[/math] и [math]v[/math] одному множеству. Если нет, то объединяем множества, в которых лежат [math]u[/math] и [math]v[/math], и добавляем ребро [math]uv[/math] к [math]F[/math].

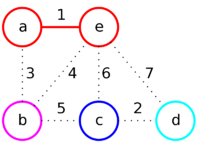
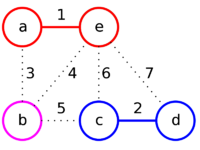
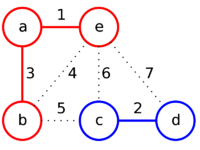
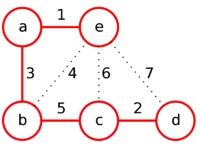
Пример

Отсортируем рёбра по их весам и рассмотрим их в порядке возрастания.

Рёбра (в порядке их просмотра)	ae	cd	ab	be	bc	ec	ed
Веса рёбер	[math]1[/math]	[math]2[/math]	[math]3[/math]	[math]4[/math]	[math]5[/math]	[math]6[/math]	[math]7[/math]

Изображение	Описание
	Первое ребро, которое будет рассмотрено - ae, так как его вес минимальный. Добавим его к ответу, так как его концы соединяют вершины из разных множеств (a - красное и e -зелёное). Объединим красное и зелёное множество в одно (красное), так как теперь они соединены ребром.
	Рассмотрим следующие ребро - cd. Добавим его к ответу, так как его концы соединяют вершины из разных множеств (c - синие и d - голубое). Объединим синие и голубое множество в одно (синие), так как теперь они соединены ребром.
	Дальше рассмотрим ребро ab. Добавим его к ответу, так как его концы соединяют вершины из разных множеств (a - красное и b - розовое). Объединим красное и розовое множество в одно (красное), так как теперь они соединены ребром.
	Рассмотрим следующие ребро - be. Оно соединяет вершины из одного красного множества, поэтому перейдём к следующему ребру bc Добавим его к ответу, так как его концы соединяют вершины из разных множеств (b - красное и c - синие). Объединим красное и синие множество в одно (красное), так как теперь они соединены ребром.
	Теперь рёбра ec и ed соединяют вершины из одного красного множества. Всё рёбра были рассмотрены, поэтому алгоритм завершает работу. Полученный граф - минимальное остовное дерево

Асимптотика

Сортировка [math]E[/math] займет [math]O(E\log E)[/math].
Работа с DSU займет [math]O(E\alpha(V))[/math], где [math]\alpha[/math] - обратная функция Аккермана, которая не превосходит 4 во всех практических приложениях и которую можно принять за константу.
Алгоритм работает за [math]O(E(\log E+\alpha(V))) = O(E\log E) = O(E\log V^2) = O(E\log V)[/math].

Литература

• Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест, Рональд Л., Штайн Клиффорд Алгоритмы: построение и анализ, 2-е издание. Пер. с англ. — М.:Издательский дом "Вильямс", 2010. — 1296 с.: ил. — Парал. тит. англ. — ISBN 978-5-8459-0857-5 (рус.)

См. также

• Алгоритм Прима