Постановка задачи
Рассмотрим задачу:
- Дано [math]n[/math] работ и [math]2[/math] станка.
- Для каждой работы известно её время выполнения на каждом станке.
Требуется минимизировать время окончания всех работ, если каждую работу необходимо выполнить на обоих станках.
Описание алгоритма
Пусть [math]a_{i}[/math] — время выполнения [math]i[/math]-ой работы на первом станке, а [math]b_{i}[/math] — на втором.
- Разобьём все работы на два множества: [math]I = \{i \mid a_{i} \le b_{i}; i = 1, \dots, n\}[/math] и [math]J = \{i \mid a_{i} \gt b_{i}; i = 1, \dots, n\}[/math]
- Найдем [math]a_{x} = \max \{a_{i} \mid i \in I\}[/math] и [math]b_{y} = \max \{b_{i} \mid i \in J\}[/math]
- Построим целевую функцию: [math]C_{max} = \max \{\sum \limits_{i = 1}^{n} a_i, \sum \limits_{i = 1}^{n} b_i, \max \limits_{i = 1}^{n}\{a_i + b_{i}\}\}[/math].
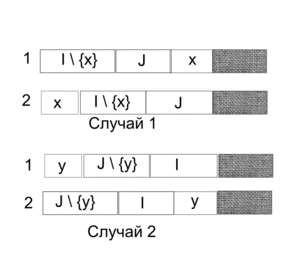
- Рассмотрим 2 случая. Первый случай, когда [math]a_{x} \le b_{y}[/math]. Будем строить расписание с двух концов:
- Строим расписание слева: выполняем на первом станке все работы из [math]I \setminus \{x\}[/math], а на втором выполняем первой работу [math]x[/math], затем [math]I \setminus \{x\}[/math].
- Теперь, упираясь в левую границу, зная значение [math]C_{max}[/math], можно построить расписание справа: выполняем на первом станке все работы из [math]J[/math], затем [math]x[/math], а для второго выполняем работы из [math]J[/math]
Второй случай рассматривается аналогично: все работы и станки меняются местами.
Доказательство корректности алгоритма
| Теорема: |
Расписание, построенное данным алгоритмом, является корректным и оптимальным. |
| Доказательство: |
| [math]\triangleright[/math] |
|
Чтобы доказать корректность, надо доказать, что на каждом станке никакая из работ не пересекается, и что каждая работа в каждый момент времени выполняется только на одном станке.
Первое утверждение вытекает из того, что мы строили расписание, опираясь на [math]C_{max}[/math]. Из построения [math]C_{max} \ge \sum \limits_{i = 1}^{n}a_{i}, \sum \limits_{i = 1}^{n}b_{i}[/math], следовательно на каждом станке нет пересечения работ.
Докажем теперь второе утверждение. У нас имеется 3 блока: [math] I \setminus \{x\}, \{x\}, J[/math].
- Для блока [math] \{x\}[/math] пересечения отсутствуют из того, что [math] C_{max} \ge a_{x}+b_{x}[/math], а этот блок выполняется с разных концов станков, значит он не может пересекаться.
- Для блока [math] I \setminus \{x\}[/math] рассмотри сумму:
[math]\sum \limits_{i = 1}^k a_{i} \le \sum \limits_{i = 1}^k b_{i} \le \sum \limits_{i = 1}^{k - 1} b_{i} + b_{x}[/math]
Это неравенство следует из выбора [math]I[/math] и из того, что [math]b_{x} \ge a_{x} \ge a_{i}, \forall i \in I[/math].
Получили, что этот блок тоже не пересекается.
- Для блока [math]J[/math] рассмотри сумму:
[math]\sum \limits_{i = 1}^k b_{i} \le \sum \limits_{i = 1}^k a_{i} \le \sum \limits_{i = 1}^{k - 1} a_{i} + a_{x}[/math]
Это неравенство следует из выбора [math]J[/math] и из того, что [math]a_{x} \ge a_{i}, \forall i \in I[/math].
Получили, что этот блок тоже не пересекается.
Итого мы доказали корректность.
Оптимальность вытекает, из того, что [math]C_{max}[/math] не может быть меньше [math]\sum \limits_{i = 1}^{n} a_i, \sum \limits_{i = 1}^{n} b_i, \max \limits_{i = 1}^{n}\{a_i + b_{i}\}[/math], а из построения оно равно максимум из них. |
| [math]\triangleleft[/math] |
Псевдокод
[math]I \leftarrow \varnothing [/math]
[math]J \leftarrow \varnothing [/math]
for [math]i = 1 \dots n[/math]
if [math]a_{i} \le b{i}[/math]
[math] I \leftarrow I \cup \{i\} [/math]
else
[math] J \leftarrow J \cup \{i\} [/math]
Найти [math]x[/math], где [math]a_{x} = \max \limits_{i \in I} \{a_{i}\}[/math]
Найти [math]y[/math], где [math]b_{y} = \max \limits_{i \in J} \{b_{i}\}[/math]
if [math]a_{x} \gt b_{y}[/math]
Поменять местами первый и второй станок
Пересчитать [math]I, J, x[/math]
Запомнить, что поменяли
[math]time1 \leftarrow 0[/math]
shed2[x] [math]\leftarrow 0[/math]
[math]time2 \leftarrow b_{x}[/math]
Для всех [math]i \in I \setminus \{x\}[/math]
sched1[i] [math]\leftarrow time1[/math]
[math]time1 \leftarrow time1 + a_{i}[/math]
sched2[i] [math]\leftarrow time2[/math]
[math]time2 \leftarrow time2 + b_{i}[/math]
Для всех [math]i \in J[/math]
sched1[i] [math]\leftarrow time1[/math]
[math]time1 \leftarrow time1 + a_{i}[/math]
sched2[i] [math]\leftarrow time2[/math]
[math]time2 \leftarrow time2 + b_{i}[/math]
sched1[x] [math]\leftarrow time1[/math]
[math]time1 \leftarrow time1 + a_{x}[/math]
[math]C_{max} \leftarrow \max\{time1, time2\}[/math]
if станки меняли местами
поменять их обратно
Сложность алгоритма
Каждое из множеств в сумме содержит [math]n[/math] элементов. Следовательно, чтобы найти максимум в каждом из множеств нам потребуется [math]O(n)[/math] операций, чтобы составить расписание для каждой работы из множества нам потребуется так же [math]O(n)[/math] операций. Получаем сложность алгоритма [math]O(n)[/math].