Дерево отрезков. Построение

Дерево отрезков — это структура данных, которая позволяет за асимптотику [math]O(\log n)[/math] реализовать любые операции, определяемые на моноиде. Например, следующего вида: нахождение суммы (задача RSQ), минимума или максимума (задача RMQ) элементов массива в заданном отрезке ([math]a[i...j][/math], где [math]i[/math] и [math]j[/math] поступают на вход алгоритма)

При этом дополнительно возможно изменение элементов массива: как изменение значения одного элемента, так и изменение элементов на целом подотрезке массива, например разрешается присвоить всем элементам [math]a[i...j][/math] какое-либо значение, либо прибавить ко всем элементам массива какое-либо число. Структура занимает [math]O(n)[/math] памяти, а ее построение требует [math]O(n)[/math] времени.

Структура

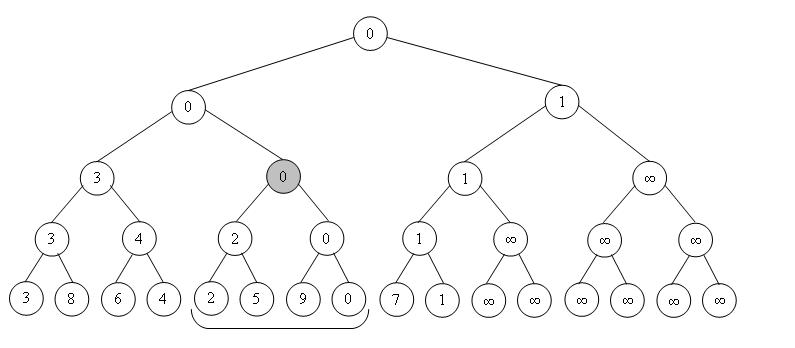
Структура представляет собой дерево, листьями которого являются элементы исходного массива. Другие вершины этого дерева имеют по 2 ребёнка и содержат результат операции от своих детей (например минимум или сумму). Таким образом, корень содержит результат искомой функции от всего массива [math][0...n-1][/math], левый ребёнок корня содержит результат функции на [math][0...n/2][/math], а правый, соответственно результат на [math][n/2+1...n-1][/math]. И так далее, продвигаясь вглубь дерева.

Построение дерева

Пусть исходный массив [math]a[/math] состоит из [math]n[/math] элементов. Для удобства построения увеличим длину массива [math]a[/math] так, чтобы она равнялась ближайшей степени двойки, т.е. [math]2^k[/math], где [math]2^k \ge n[/math]. Это сделано, для того чтобы не допустить обращение к несуществующим элементам массива при дальнейшем процессе построения. Пустые элементы необходимо заполнить нейтральными элементами моноида. Тогда для хранения дерева отрезков понадобится массив [math]t[/math] из [math]2^{k+1}[/math] элементов, поскольку в худшем случае количество вершин в дереве можно оценить суммой [math]n+n/2+n/4...+1 \lt 2n[/math], где [math]n=2^k[/math]. Таким образом, структура занимает линейную память.

Процесс построения дерева заключается в заполнении массива [math]t[/math]. Заполним этот массив таким образом, чтобы [math]i[/math]-й элемент являлся бы значением функции (для каждой конкретной задачи своей) от элементов c номерами [math]2i+1[/math] и [math]2i+2[/math], то есть родитель являлся значением функции своих сыновей. Один из вариантов — делать рекурсивно. Пусть у нас имеются исходный массив [math]a[/math], а также переменные [math]tl[/math] и [math]tr[/math], обозначающие границы текущего полуинтервала. Запускаем процедуру построения от корня дерева отрезков ([math]i=0[/math], [math]tl=0[/math], [math]tr=n[/math]), а сама процедура построения, если её вызвали не от листа, вызывает себя от каждого из двух сыновей и суммирует вычисленные значения, а если её вызвали от листа — то просто записывает в себя значение этого элемента массива (Для этого у нас есть исходный массив [math] a [/math]). Асимптотика построения дерева отрезков составит, таким образом, [math]O(n)[/math].

Выделяют два основных способа построения дерева отрезков: построение снизу и построение сверху. При построении снизу алгоритм поднимается от листьев к корню (Просто начинаем заполнять элементы массива [math]t[/math] от большего индекса к меньшему, таким образом при заполнении элемента [math] i [/math] его дети [math]2i+1[/math] и [math]2i+2[/math] уже будут заполнены, и мы с легкостью посчитаем функцию от них), а при построении сверху спускается от корня к листьям. Особенные изменения появляются в реализации запросов к таким деревьям отрезков.

Реализация построения сверху:

TreeBuild(a[], i, tl, tr)
// Мы находимся в элементе с номером i, который отвечает за полуинтервал [tl, tr)
 if (tl = tr) return;
 if (tr - tl = 1)
    t[i] = a[tl];
 else
    tm = (tl + tr) / 2; //середина отрезка
    TreeBuild(a, 2 * i + 1, tl, tm);
    TreeBuild(a, 2 * i + 2, tm, tr);
    t[i] = f(t[2 * i + 1], t[2 * i + 2]);

Реализация построения снизу:

TreeBuild(a[])
 for i = n - 1 .. 2 * n - 1
  t[i] = a[i - n - 1]
 for i = n - 2 .. 0
  t[i] = f(t[2 * i + 1], t[2 * i + 2])

Персистентное дерево отрезков

Определение:

Персистентной(persistent) называется такая структура данных, которая хранит все свои промежуточные версии.

Определение:

Полностью персистентной(fully persistent) называется такая персистентная структура данных, что разрешено изменять любую её версию и делать запросы к любой её версии.

На основе дерева отрезков можно построить полностью персистентную структуру данных.

Структура дерева

Для реализации персистентного дерева отрезков удобно несколько изменить структуру дерева:

будем использовать явные указатели [math]L[/math] и [math]R[/math] для дочерних элементов и [math]P[/math] для родительского узла
заведем массив [math]roots[][/math], в котором [math]roots[i][/math] указывает на корень дерева отрезков версии [math]i[/math]

Построение

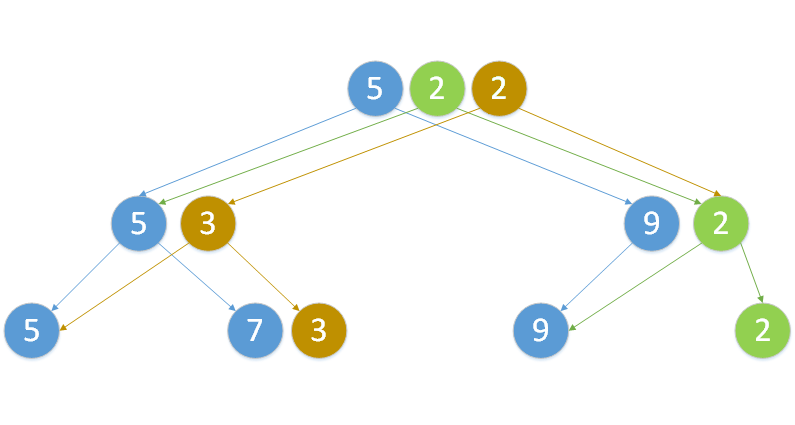
Для построения персистентного дерева отрезков из [math]n[/math] элементов необходимо применить [math]n[/math] раз операцию добавления элемента к последней версии дерева. Для того, чтобы добавить новый элемент к [math]k[/math]-ой версии дерева, необходимо проверить, является ли оно полным бинарным. Если да, то создадим новый корень, левым сыном сделаем [math]roots[k][/math]. Иначе, оставим корень таким же, как и в исходной версии. Далее, спускаясь от корня к первому свободному листу, будем создавать несуществующие узлы и клонировать существующие, изменяя указатель на родителя на предыдущий созданный узел. После этого в новой ветке необходимо обновить значение функции и некоторые указатели дочерних элементов. Поэтому, возвращаясь из рекурсии, будем менять один указатель на только что созданную или скопированную вершину, а также обновим значение функции поместим новый корень в список корней. После этой операции в дереве появится новая версия, содержащая вставленный элемент.

Изменение элемента

Воспользуемся аналогичной схемой, что и при вставке элемента. Для этого найдем в дереве требуемый элемент, скопируем его, изменим значение, и, поднимаясь по дереву, будем клонировать узлы, меняя один из указателей и пересчитывая значение функции. Новый корень добавим в список корней.

Псевдокод


 addElement(Tree, ver, x)
   if Tree.isFullBinary(ver)
     Node tmpRoot = new Node();
     roots[Tree.countOfVersions++ + 1] = recAdd(tmpRoot, null, 0, 2 * Tree.size(ver), x, Tree.size(ver) + 1); 
   else 
     // k : 2 ^ (k - 1) <= Tree.size(ver) < 2 ^ k
     roots[Tree.countOfVersions++ + 1] = recAdd(roots[ver], null, 0, 2 ^ k, x, Tree.size(ver) + 1);
 
 Node recAdd(node, parent, l, r, x, n)
   // Мы находимся в узле node, который отвечает за полуинтервал (l, r]
   if r - l == 1
     return new Node(parent, x)
   m = (l + r) / 2;
   if node == null
     Node tmp = new Node(parent);
     node = tmp;
   else 
     Node tmp = node.clone();
     tmp.parent = parent;
   if n <= m
     tmp.L = recAdd(node.L, tmp, l, m, x, n);
   else 
     tmp.R = recAdd(node.R, tmp, m, r, x, n);
   tmp.valueOfFunction = f(tmp.L, tmp.R);
   return tmp;

 Node change(Tree, parent, node, l, r, i, x)
   //изменить i-ый элемент на x
   if r - l == 1
     return new Node(x);
   else
     m = (l + r) / 2;
     Node tmp = node.clone();
     tmp.parent = parent;
     if i <= m
       tmp.L = change(Tree, tmp, node.L, l, m, i, x);
     else
       tmp.R = change(Tree, tmp, node.R, m, r, i, x);
     tmp.valueOfFunction = f(tmp.L, tmp.R);
     if(node.parent == null)
       roots[Tree.countOfVersions++ + 1] = tmp;
     return tmp;

Здесь функции [math]recAdd()[/math] и [math]change()[/math] возвращает указатель на узел новой ветки.