Алгоритм Балабана

Материал из Викиконспекты
Перейти к: навигация, поиск
Эта статья находится в разработке!

Алгоритм Балабана — детерминированный алгоритм, позволяющий по множеству отрезков на плоскости получить множество точек, в которых эти отрезки пересекаются.

Введение

Решение задачи по поиску множества пересечений отрезков является одной из главных задач вычислительной геометрии. Тривиальный детерминированный алгоритм имеет временную сложность [math]O(n^2)[/math], и его суть заключается в проверке попарного пересечения отрезков. Сложнее, но эффективнее алгоритм Бентли-Оттмана [1] с оценкой сложности [math]O((n + k)\ log(n)+k)[/math], в основе которого лежит метод заметающей прямой. Алгоритм, предложенный Чазелле и Едельсбруннером [2], имеет лучшую оценку [math]O(n\ log(n) + k)[/math], но в отличие от предыдущих методов требует квадратичной памяти. Оптимальный детерминированный алгоритм был предложен Балабаном [3] с временной оценкой сложности [math]O(n\ log(n) + k)[/math] и [math]O(n)[/math] памяти, где К - число пересекающихся отрезков. При количестве отрезков равным 2000 и большому количеству пересечений целесообразно использовать алгоритм Балабана. Однако в результате громоздкости и высокой сложности реализации алгоритма в большинстве практических задач используется алгоритм заметающей прямой Бентли-Оттмана.

Основные понятия

Введем некоторые обозначения. Пусть [math]Int(S)[/math] - множество всех точек пересечения отрезков из множества [math]S[/math], а [math]K = |Int(S)|[/math] - количество таких пересечений ;
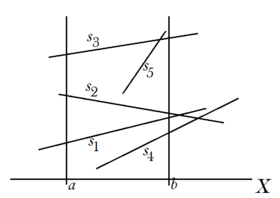
Через [math]\langle a, b \rangle[/math] обозначим вертикальную полосу, которая ограничена прямыми [math]x = a[/math] и [math]x = b[/math], а через [math]s[/math] — отрезок с вершинами в точках с абсциссами [math]l[/math] и [math]r[/math].
Рассмотрим взаимное расположение вертикальной полосы [math]\langle a, b \rangle[/math] и отрезка [math]s[/math].


Определение:
Будем говорить, что отрезок [math]s[/math], с вершинами в точках с абсциссами [math]l[/math] и [math]r[/math] :

- содержит(span) полосу [math]\langle a, b \rangle[/math], если [math]l \le a \le b \le r[/math];
- внутренний(inner) для полосы [math]\langle a, b \rangle[/math], если [math]a \lt l \lt r \lt b[/math];

- пересекает(cross) полосу [math]\langle a, b \rangle[/math] в других случаях.


Определение:
Два отрезка [math]s_1[/math] и [math]s_2[/math] называются пересекающимися внутри полосы [math]\langle a, b \rangle[/math], если их точка пересечения лежит в пределах этой полосы.
Для двух множеств отрезков [math]S[/math] и [math]S'[/math] определим множество [math]Int(S, S')[/math] как [math]\{ {s, s'} | (s \in S, s' \in S') \& (s \ intersect \ s') \}[/math].
[math]D = ((s_1, s_2, s_3), \langle a, b \rangle)[/math], [math]Loc(D, s_4) = 0[/math], [math]Loc(D, s_5) = 2[/math] или [math]3[/math], [math]Int(D, \{s_4,\ s_5\}) = \{\{s_3,\ s_5\}\}[/math]

Обозначения [math]Int_{a, b}(S)[/math] и [math]Int_{a, b}(S, S')[/math] будут использоваться для описания подмножеств [math]Int(S)[/math] и [math]Int(S, S')[/math], состоящих из пересекающихся пар отрезков в пределах полосы [math]\langle a, b \rangle[/math]. Далее скобки [math]\{\}[/math] используются для определения неупорядоченных наборов, а скобки [math]()[/math] используются для определения упорядоченных множеств.

Введем отношение порядка на множестве отрезков [math]s_1 \lt _b s_2[/math] если оба отрезка пересекают вертикальную линию [math]x = a[/math] и точка пересечения этой прямой с отрезком [math]s_1[/math] лежит ниже точки пересечения с [math]s_2[/math].


Определение:
Лестница [math]D[/math] — это пара [math](Q, \langle a, b \rangle)[/math], в которой отрезки из множества [math]Q[/math] удовлетворяют следующим условиям :

− любой отрезок из [math]Q[/math] содержит полосу [math]\langle a, b \rangle[/math];
− нет пересечений отрезков внутри лестницы;
− [math]Q[/math] упорядочена по отношению [math]\lt _a[/math].

Часть отрезков лестницы внутри полосы будем называть ступеньками.


Определение:
Будем называть лестницу [math]D[/math] полностью соотносимой множеству отрезков [math]S[/math], если каждый отрезок из [math]S[/math] либо не пересекает полосу [math]\langle a, b \rangle[/math], либо пересекает хотя бы одну из ступенек из множества [math]D[/math].


Лемма:
Если лестница [math]D[/math] полностью соотносима множеству отрезков [math]S[/math], где [math]S[/math] состоит из отрезков, пересекающих полосу [math]\langle a, b \rangle[/math], тогда [math]|S| \le Ends_{a, b}(S) + |Int(D, S)|[/math],
где [math]Ends_{a, b}(S)[/math] это число вершин отрезков [math]S[/math], находящихся в пределах полосы [math]\langle a, b \rangle[/math].


Определение:
Если точка [math]p[/math] отрезка [math]s[/math] лежит между ступеньками [math]i[/math] и [math]i + 1[/math], тогда число [math]i[/math] называется местоположением [math]s[/math] на лестнице [math]D[/math] и обозначается как [math]Loc(D, s)[/math]


Утверждение:
Имея лестницу [math]D = (Q, \langle a, b \rangle)[/math] и множество отрезков [math]S[/math], множество [math]Int(D, S)[/math] можно найти за время [math]O(|S| log|Q| + |Int(D, S)|)[/math].
Однако, если [math]S’[/math] упорядочено отношением [math]\lt _x[/math], где [math]x \in [a, b][/math], тогда можно найти [math]Int(D, S)[/math] за время [math]O(|S| + |Q| + |Int(D, S)|)[/math].

Алгоритм

Введем несколько дополнительных функций, чтобы упростить основной алгоритм:

Split

Функция [math]Split[/math] разделяет входное множество отрезков [math]L[/math], пересекающих некоторую полосу [math]\langle a, b \rangle[/math], на подмножества [math]Q[/math] и [math]L'[/math] так, что лестница [math](Q, \langle a, b \rangle)[/math] полностью соотносима множеству отрезков [math]L'[/math]. 

Пусть [math]L = (s_1 ,..., s_k)[/math], где [math]s_i \lt _b s_{i+1}[/math]
[math]Split_{a,b}(L, Q, L')[/math]
[math]\{[/math]
    [math]L' \leftarrow \varnothing; Q \leftarrow \varnothing[/math]
    For [math]j = 1,...,k[/math] do
        if отрезок [math]S_j[/math] не пересекает
        последний отрезок из [math]Q[/math] внутри полосы [math]\langle a, b \rangle[/math]
        и при этом содержит её then
            добавить [math]s_j[/math] в конец [math]Q;[/math]
        else
            добавить [math]s_j[/math] в конец [math]L’;[/math]
[math]\}[/math]

Эта функция работает за [math]O(|L|)[/math] времени.

Search In Strip

Зная [math]L[/math] мы можем найти [math]Int_{a, b}(L)[/math] и [math]R[/math] используя следующую рекурсивную функцию: 

[math]SearchInStrip_{a, b}(L, R)[/math]
[math]\{[/math]
    [math]Split(L, Q, L');[/math] 
    if [math]L' = \varnothing[/math] then
        [math]R \leftarrow Q;[/math] 
        return[math];[/math]
    Найдем [math]Int_{a, b}(Q, L');[/math]
    [math]SearchInStrip_{a, b} (L', R');[/math]
    [math]R \leftarrow Merge_b(Q, R’);[/math]
[math]\}[/math]

Здесь, [math]Merge_x(S_1, S_2)[/math] это функция объединения множеств [math]S_1[/math] и [math]S_2[/math], упорядоченных по отношению [math]\lt _x[/math]. Время выполнения [math]SearchInStrip[/math] эквивалентно сумме времён каждого её запуска. Очевидно, что время работы [math]i[/math]-той функции, будет равно [math]O(|L_i| + |Int_{a, b}(Q_i, {L_i}')|)[/math], где [math]L_i, Q_i, {L_i}'[/math] это соответствующие наборы [math](L_0 = L, L_{i+1} = {L_i}')[/math].

Учитывая лемму, заключаем, что функция [math]SearchInStrip_{a, b}(L, R)[/math] работает за [math]O(|L| + |Int_{a, b}(L)|)[/math].

Предположим, что все отрезки лежат в полосе [math]\langle a, b \rangle[/math]. Таким образом в самом начале у нас есть пара [math](S, \langle a, b, \rangle)[/math]. Что же дальше происходит: множество [math]S[/math] распадается в подмножества [math]Q[/math] и [math]S'[/math], после чего лестница [math]D = (Q, \langle a, b \rangle)[/math] становится полностью соотносимой множеству [math]S'[/math]. Необходимо найти пересечения отрезков из [math]D[/math] и [math]S'[/math], затем, все пересечения в [math]S'[/math]. Чтобы найти пересечения отрезков в [math]S'[/math], мы режем полосу [math]\langle a, b \rangle[/math] и множество [math]S'[/math] по вертикале [math]x = c[/math] на полосы [math]\langle a, с \rangle[/math], [math]\langle с, b \rangle[/math] и множества [math]S'_{ls}[/math], [math]S'_{rs}[/math] соответственно, где c является медианой вершин отрезков, между [math]a[/math] и [math]b[/math]. Затем мы рекурсивно вызываем функцию к парам [math](S'_{ls}, \langle a, c \rangle)[/math] и [math](S'_{rs}, \langle c, b \rangle)[/math]. Ключевым является тот факт, что согласно лемме [math]|S'| \le Ends_{a, b}(S') + |Int(D, S')|[/math], таким образом, число дополнительных отрезков, появляющихся после разрезаний пропорционально числу найденных пересечений.

Пункт подробностей =)

Давайте разберемся с алгоритмом более подробнее:

Не умаляя общности, предположим, что все пересечения и вершины отрезков имеют разные абсциссы. В конечном счете, их можно будет поставить на свое место введением дополнительных свойств. Рассматриваем целые координаты на промежутке [math]\[1, 2N\][/math].

Итак, пусть [math]p_i{[/math] So, let p,, i and s(i) be the ith endpoint its abscissa and the segment to which it belongs, respectively.

Основная задача нашего алгоритма, это рекурсивная функция [math]TreeSearch[/math]. Мы соединяем каждый вызов функции с узлом некоего двоичного дерева, именуемого далее рекурсивным деревом. Мы отмечаем все значения, множества и параметры вызова соответствующим узлом. As a result we shall analyze our algorithm examining the recursion tree. Let RT be the set of all nodes of recursion tree, and V be the set of internal nodes. We shall define some values, sets and notations inside the bodies of procedures.

procedure IntersectingPairs(SO ). Sort the 2N endpoints by abscissa and find p,, s(i), i= 1,,..,2N; ST := S.; TreeSearch(S,, 1, 2N); end procedure. procedure TreeSearch(S., b, e). Ife–b=l then L. =sort S. by <b; SearchInStripb,. (LU, R.); exit; endif Split S. into Q. and S: so that staircase Du := (Qv, (b, e)) be complete relative to S:; Find lnt(DV , S:); c:= L(b + e)/2J; Place segments of S: crossing the strip (b, c) into S[~(V ) and the strip (c, e) into s~.(~); TreeSearch(S1.(V), b, c); TreeSearch(ST,(V), c, e); end procedure.

Примечания

  1. ↑ Алгоритм Бентли-Оттмана
  2. ↑ An optimal algorithm for intersecting line segments in the plane
  3. ↑ I.J. Balaban. An optimal algorithm for finding segments intersections. In Proceedings of the Eleventh Annual Symposium on Computational Geometry, ACM Press, New York, 1995. - pp. 211–219.

Литература

Т.Вознюк, В.Терещенко — К построению эффективного решения задачи пересечения отрезков
Ф.Препарата, М.Шеймос — Вычислительная геометрия

Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Алгоритм_Балабана&oldid=33017»