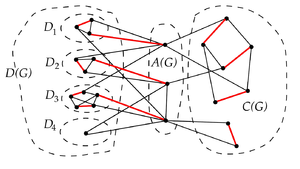
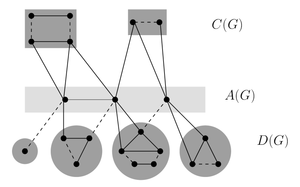
Декомпозиция Эдмондса-Галлаи

В этом направлении много усилий приложили Вильям Томас Татт (William Thomas Tutte), Клауд Берж(Claude Brege), Джек Эдмондс(Jack Edmonds) и Тибор Галлаи(Tibor Gallai).

Определение:

[math]\mathrm{odd}(G)[/math] - количество компонент связности нечетного размера в [math] G[/math].

Определение:

Дефицитом графа G мы будем называть величину: [math]\mathrm{def}(G) = |V| - 2\alpha (G)[/math], где [math]\alpha (G)[/math] - размер максимального паросочетания в [math]G[/math], а [math]V(G)[/math] - множество вершин графа [math]G[/math]

Теорема (Бержа):

Для любого графа G выполняется: [math]\mathrm{def}(G) = \max\limits_{S \subset V(G)} \{\mathrm{odd}(G - S) - |S|\}.[/math]

Теорема (Татта-Бержа):

Дан граф [math]G[/math], размер максимального паросочетания в нем равен: [math]\mathrm{ \alpha} (G) = \min\limits_{U \in V} \{1/2(|V|-|U|-\mathrm{odd}(G-U)\} [/math]

Определение:

Множество [math]S \subset V (G)[/math], для которого [math]\mathrm{odd}(G - S) - |S| = \mathrm{def}(G) [/math], называется барьером.

Определение:

Пусть [math]X \subset V [/math]. Множeство соседей (англ. neighbors)[math]X[/math] определим формулой: [math]N(X)= \{ y \in V: (x,y) \in E \}[/math]

Структурная теорема Эдмондса-Галлаи

Определение:

Необходимые определения: Пример. Рёбра из паросочетания выделены красным [math]D(G) = \{v \in V |[/math] существует максимальное паросочетание, не покрывающее [math] v\}[/math] [math]A(G) = N(D(G)) \setminus D(G)[/math] [math]C(G) = V \setminus( D(G) \bigcup A(G) )[/math] [math] \alpha (G) [/math] - размер максимального паросочетания в [math]G[/math] (англ. maximum matching in G)

Определение:

Граф [math]G[/math] называется фактор-критическим (англ. factor-critical graph), если для любой вершины [math]v \in G[/math] в графе [math]G \setminus {v}[/math] существует совершенное паросочетание.

Теорема (Галлаи):

[math]G[/math] - фактор-критический граф [math] \Leftrightarrow [/math] [math]G[/math] - связен и для любой вершины [math]u \in V(G) [/math] выполняется равенство [math] \alpha (G - u) = \alpha (G)[/math].

Лемма (Галлаи, о стабильности (англ. stability lemma)):

Пусть [math] a \in A(G).[/math] Тогда: [math]D(G - a) = D(G)[/math] [math]A(G - a) = A(G) \setminus \{a\}[/math] [math]C(G - a) = C(G)[/math] [math] \alpha (G - a) = \alpha (G) - 1.[/math]

Доказательство:

[math]\triangleright[/math]

Достаточно доказать, что [math]D(G - a) = D(G)[/math]. покажем, что [math]D(G - a) \supset D(G)[/math] : Пусть [math]u \in D(G)[/math]. Тогда существует максимальное паросочетание [math]M_u[/math] графа [math]G[/math], не покрывающее [math]u[/math]. Поскольку любое максимальное паросочетание графа [math]G[/math] покрывает a, то [math] \alpha (G - a) = \alpha (G) - 1 [/math] и более того, если, для некоторой вершины [math]x \in D(G)[/math], [math]ax \in M_u[/math], то [math]M_u \setminus {ax} [/math] - максимальное паросочетание графа [math] G - a [/math], не покрывающее [math] u [/math]. Таким образом, [math]D(G - a) \supset D(G) [/math]. 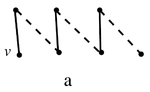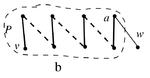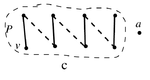покажем, что [math] D(G - a) \subset D(G)[/math]: Предположим, что существует максимальное паросочетание [math]M'[/math] графа [math] G - a[/math], не покрывающее вершину [math]v[/math] [math] \notin D(G)[/math]. Пусть [math] w \in D(G) [/math] - смежная с [math] a \in A(G)[/math] вершина, а [math] M_w [/math]- максимальное паросочетание графа [math] G [/math], не покрывающее [math] w [/math]. Так как [math]v[/math] [math] \notin D(G) [/math], максимальное паросочетание [math] M_w [/math] покрывает вершину [math]v[/math]. Рассмотрим граф [math] H = G(M_w \bigcup M') [/math] - очевидно, он является объединением нескольких путей и чётных циклов. Пусть [math] U [/math] - компонента связности графа [math] H [/math], содержащая [math]v[/math]. Так как [math] deg_H(v) = 1 [/math](степень вершины), то [math] P = H(U) [/math] - путь с началом в вершине [math]v[/math]. В пути [math]P[/math] чередуются рёбра из [math] M_w[/math] и [math]M' [/math], причём начинается путь ребром из [math]M_w [/math]. Так как [math] deg_H(a) = 1 [/math], то вершина a либо не принадлежит пути [math]P[/math], либо является её концом (в этом случае последнее ребро пути принадлежит паросочетанию [math] M_w[/math]). Рассмотрим несколько случаев: случай а a. Путь [math]P[/math] кончается ребром из [math] M'[/math] (см. рисунок) Рассмотрим паросочетание [math]M_v = M_w \oplus E(P)[/math] (симметрическая разность [math] M_w[/math] и [math]E(P)[/math]. то есть, рёбра, входящие ровно в одно из двух множеств). Очевидно, [math]M_v[/math] - максимальное паросочетание графа [math]G[/math], не покрывающее [math]v[/math], поэтому [math] v \in D(G)[/math], противоречие. случай b b. Путь [math]P[/math] кончается ребром из [math] M_w[/math], вершина a - конец пути [math]P[/math]. (см.рисунок) Рассмотрим паросочетание [math]M_v∗ = (M_w \oplus E(P)) \bigcup \{aw\} [/math]. Тогда [math] M_v∗ [/math] - максимальное паросочетание графа [math] G [/math], не покрывающее [math] v [/math], поэтому [math] v \in D(G) [/math], противоречие. случай c c. Путь [math] P [/math] кончается ребром из [math] M_w, a \in V(P) [/math] (см. рисунок) Рассмотрим паросочетание [math] M'' = M \oplus E(P) [/math]. Тогда [math] |M''| = |M'| + 1 [/math], причём [math]M'' \subset E(G - a)[/math]. Противоречие с максимальностью паросочетания [math]M'[/math]. Таким образом, наше предположение невозможно и [math]D(G - a) \subset D(G)[/math]. А значит, [math]D(G - a) = D(G)[/math].

[math]\triangleleft[/math]

Теорема (Галлаи, Эдмондс):

Пусть G - граф, [math]U_1,{...},U_n[/math] - компоненты связности графа [math]G(D(G))[/math], [math]D_i = G(U_i), C = G(C(G))[/math]. тогда: Граф [math]C[/math] имеет совершенное паросочетание. Графы [math]D_1,{...},D_n[/math] - фактор-критические. Любое максимальное паросочетание [math]M[/math] графа [math]G[/math] состоит из совершенного паросочетания графа [math]C[/math], почти совершенных паросочетаний графов [math]D_1,{...},D_n[/math] и покрывает все вершины множества [math]A(G)[/math] рёбрами с концами в различных компонентах связности [math]U_1,{...},U_n[/math] [math]\mathrm{def}(G) = n - |A(G)|, 2\mathrm{\alpha}(G) = v(G) + |A(G)| - n[/math].

Доказательство:

[math]\triangleright[/math]

Пример Последовательно удаляя вершины множества[math] A = A(G)[/math], по лемме о стабильности мы получим: [math]D(G - A) = D(G),[/math] [math]A(G - A) = \O, [/math] [math]C(G - A) = C(G),[/math] [math]\alpha (G - A) = \alpha (G) - |A|.[/math] Это означает, что не существует рёбер, соединяющих вершины из [math]C(G - A)[/math] и [math]D(G - A)[/math]. Каждое максимальное паросочетание [math]M'[/math] графа [math]G - A[/math] покрывает все вершины множества [math]C(G)[/math], поэтому [math]M'[/math] содержит совершенное паросочетание графа [math]C[/math]. Тем самым, мы доказали пункт 1). Из формулы [math] \alpha(G - A) = \alpha (G) - |A|[/math] следует, что [math]U_1,{...},U_n[/math]- компоненты связности графа [math]G - A[/math]. Для любой вершины [math]u \in U_i[/math] существует максимальное паросочетание [math]M_u[/math] графа [math]G - A[/math], не содержащее [math]u[/math]. Так как [math]U_i[/math] - компонента связности графа [math]G - A[/math], паросочетание [math]M_u[/math] содержит максимальное паросочетание графа [math]D_i[/math] (разумеется, не покрывающее вершину [math]u[/math]). Следовательно, [math] \alpha (D_i) = \alpha (D_i - u) [/math] и по теореме Галлаи(выше) мы получаем, что граф [math]D_i[/math] - фактор-критический. Пусть [math]M[/math] - максимальное паросочетание графа [math]G[/math], а [math]M'[/math] получено из [math]M[/math] удалением всех рёбер, инцидентных вершинам множества [math]A[/math]. Тогда [math]|M'| \ge |M| - |A|[/math] и по формуле [math] \alpha (G - A) = \alpha (G) - |A|[/math] понятно, что [math]M'[/math] - максимальное паросочетание графа [math]G - A[/math]. Более того, из [math] \alpha (G - A) = \alpha (G) - |A|[/math] следует [math]|M'| = |M| - |A|[/math], а значит, все вершины множества [math]A[/math] покрыты в [math]M[/math] различными рёбрами. Так как [math]M'[/math] - максимальное паросочетание графа [math]G - A[/math], то по пунктам 1) и 2) очевидно, что [math]M'[/math] содержит совершенное паросочетание графа [math]C[/math] и почти совершенные паросочетания фактор-критических графов [math]D_1,{...},D_n[/math]. Значит, рёбра паросочетания [math]M[/math] соединяют вершины [math]A[/math] с непокрытыми [math]M'[/math] вершинами различных компонент связности из [math]U_1,{...},U_n[/math]. Из пункта 3) сразу же следуют оба равенства пункта 4).

[math]\triangleleft[/math]

Утверждение (следствие из теоремы):

[math]A(G)[/math] - барьер графа [math]G[/math]

Источники

• Edmonds-Gallai Decomposition and Factor-Critical Graphs
• Д.В Карпов - теория графов