Пересечение полуплоскостей, связь с выпуклыми оболочками

Материал из Викиконспекты
Перейти к: навигация, поиск
Пересечение существует и выпукло, неограничено или пусто
Нужна ли нам полуплоскость [math] l'' [/math]?

Задача: есть конечное множество полуплоскотей, найти фигуру их пересечения или сообщить что оно пусто.

Для начала заметим, что если пересечение не пусто, то оно выпукло. (Доказательство — Пересечение выпуклых фигур выпукло, а полуплоскоть выпукла)

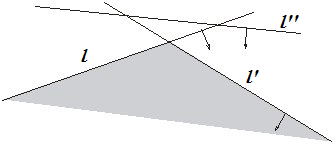
Пусть у нас прямые заданы уравнениями вида [math] Ax + By + C = 0 [/math]. Тогда предикат(см. рисунок) проверки того, что прямая [math] l'' : A''x + B''y + C'' = 0 [/math] лежит над пересечением прямых [math] l : Ax + By + C = 0 [/math] и [math] l' : A'x + B'y + C' = 0 [/math] будет равен [math] \begin{vmatrix} A & B & C \\ A' & B' & C' \\ A'' & B'' & C'' \end{vmatrix} [/math].

Докажем это. Для проверки предиката нам надо определить знак выражения [math] A''x_0 + B''y_0 + C'' [/math], где [math] (x_0, y_0) [/math] — точка пересечения прямых [math] l' [/math] и [math] l [/math]. Эту точку можно найти из уравнения [math] \begin{pmatrix} A & B\\ A' & B' \end{pmatrix} \begin{pmatrix} x_0\\ y_0 \end{pmatrix} = \begin{pmatrix} -C\\ -C' \end{pmatrix} [/math]. Решением будет [math] \begin{pmatrix} x_0\\ y_0 \end{pmatrix} = \frac{ \begin{pmatrix} B' & -B\\ -A' & A \end{pmatrix} \begin{pmatrix} -C\\ -C' \end{pmatrix}} { \begin{vmatrix} A & B\\ A' & B' \end{vmatrix} } [/math]. Подставим его в [math] A''x_0 + B''y_0 + C'' [/math] и домножим на определитель.

[math] A'' (B'; -B)(-C; -C') + B'' (-A'; A)(-C; -C') + C \begin{vmatrix} A & B \\ A' & B' \end{vmatrix} = A'' \begin{vmatrix} B' & B \\ -C' & -C \end{vmatrix} - B'' \begin{vmatrix} A' & A \\ -C' & -C \end{vmatrix} + C'' \begin{vmatrix} A & A' \\ B & B' \end{vmatrix} = \begin{vmatrix} A'' & A' & A \\ B'' & B' & B \\ -C'' & -C' & -C \end{vmatrix} = \begin{vmatrix} A & B & C \\ A' & B' & C' \\ A'' & B'' & C'' \end{vmatrix} [/math]

Таким образом если представить прямую [math] Ax + By + C = 0 [/math] как точку с координатами [math] (A, B, C) [/math], где [math] C [/math] — однородная координата, то этот предикат — всего лишь поворот, а проверка предиката — проверка очередной точки в обходе Грэхема для нахождения выпуклой оболочки.

Алгоритм:

  • Отсортировать все полуплоскости по углу наклона;
  • Запустить обход Грэхема для полуплоскостей, смотрящих вниз (с предикатом-определителем);
  • То же самое для смотрящих вверх;
  • Пересечь две цепочки.

От пересечения цепочек напрямую зависит фигура пересечения: неограниченная область получается если одна из цепочек пуста, а ограниченная — когда обе цепочки не пусты и пересекаются.

Источники

Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Пересечение_полуплоскостей,_связь_с_выпуклыми_оболочками&oldid=36389»