Splay-дерево

Сплей-дерево (Splay-tree) — это двоичное дерево поиска. Оно позволяет находить быстрее те данные, которые использовались недавно. Относится к разряду сливаемых деревьев. Сплей-дерево было придумано Робертом Тарьяном и Даниелем Слейтером в 1983 году.

Эвристики

Для того, чтобы доступ к недавно найденным данным был быстрее, надо, чтобы эти данные находились ближе к корню. Этого мы можем добиться, используя различные эвристики:

• Move to Root — совершает повороты вокруг ребра [math](x, p)[/math], где [math]x[/math] - найденная вершина, [math]p[/math] - ее предок, пока [math]x[/math] не окажется корнем дерева. Однако можно построить такую последовательность операций, что амортизированное время доступа к вершине будет [math] O(n) [/math].
• Splay — также совершает повороты, но чередует различные виды поворотов, благодаря чему достигается логарифмическая амортизированная оценка. Она будет подробно описана ниже.

Операции со splay-деревом

Splay(Tree, x)

"Splay" делится на 3 случая:

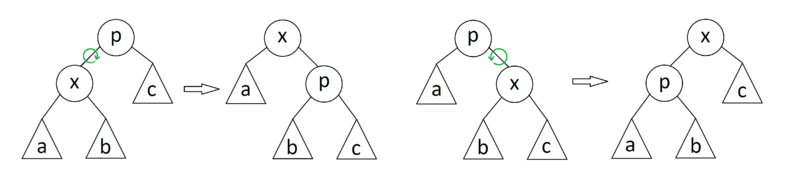
Zig

Если [math]p[/math] - корень дерева с сыном [math]x[/math], то совершаем один поворот вокруг ребра [math](x, p)[/math], делая [math]x[/math] корнем дерева. Данный случай является крайним и выполняется только один раз в конце, если изначальная глубина [math]x[/math] была нечетной.

Zig-Zig

Если [math]p[/math] - не корень дерева, а [math]x[/math] и [math]p[/math] - оба левые или оба правые дети, то делаем поворот ребра [math](p, g)[/math], где [math]g[/math] отец [math]p[/math], а затем поворот ребра [math](x, p)[/math].

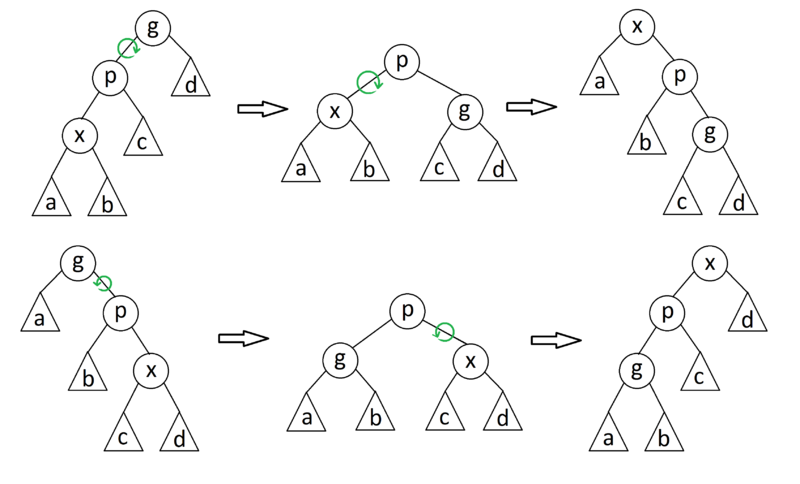
Zig-Zag

Если [math]p[/math] - не корень дерева и [math]x[/math] - левый ребенок, а [math]p[/math] - правый, или наоборот, то делаем поворот вокруг ребра [math](x, p)[/math], а затем поворот нового ребра [math](x, g)[/math], где [math]g[/math] - бывший родитель [math]p[/math].

Данная операция занимает [math]O(d)[/math] времени, где [math]d[/math] - длина пути от [math]x[/math] до корня.

Find(Tree, x)

Эта операция выполняется как для обычного бинарного дерева, только после нее запускается операция Splay.

Merge(Tree1, Tree2)

У нас есть два дерева [math]Tree1[/math] и [math]Tree2[/math], причём подразумевается, что все элементы первого дерева меньше элементов второго. Запускаем Splay от самого большого элемента в дереве [math]Tree1[/math] (пусть это элемент [math]i[/math]). После этого корень [math]Tree1[/math] содержит элемент [math]i[/math], при этом у него нет правого ребёнка. Делаем [math]Tree2[/math] правым поддеревом [math]i[/math] и возвращаем полученное дерево.

Split(Tree, x)

Запускаем Splay от элемента [math]x[/math] и возвращаем два дерева, полученные отсечением правого или левого поддерева от корня, в зависимости от того, содержит корень элемент больше или не больше, чем [math]x[/math].

Add(Tree, x)

Запускаем Split(Tree, x), который нам возвращает деревья [math]Tree1[/math] и [math]Tree2[/math], их подвешиваем к [math]x[/math] как левое и правое поддеревья соответственно.

Remove(Tree, x)

Запускаем Splay от [math]x[/math] элемента и возвращаем Merge от его детей.

Анализ операции splay

Амортизационный анализ сплей-дерева проводится с помощью метода потенциалов. Потенциалом рассматриваемого дерева назовём сумму рангов его вершин. Ранг вершины [math]x[/math] — это величина, обозначаемая [math]r(x)[/math] и равная [math]\log_2 C(x)[/math], где [math]C(x)[/math] — количество вершин в поддереве с корнем в [math]x[/math].

Лемма:

Амортизированное время операции splay вершины [math]x[/math] в дереве с корнем [math]t[/math] не превосходит [math]3r(t) - 3r(x) + 1[/math]

Доказательство:

[math]\triangleright[/math]

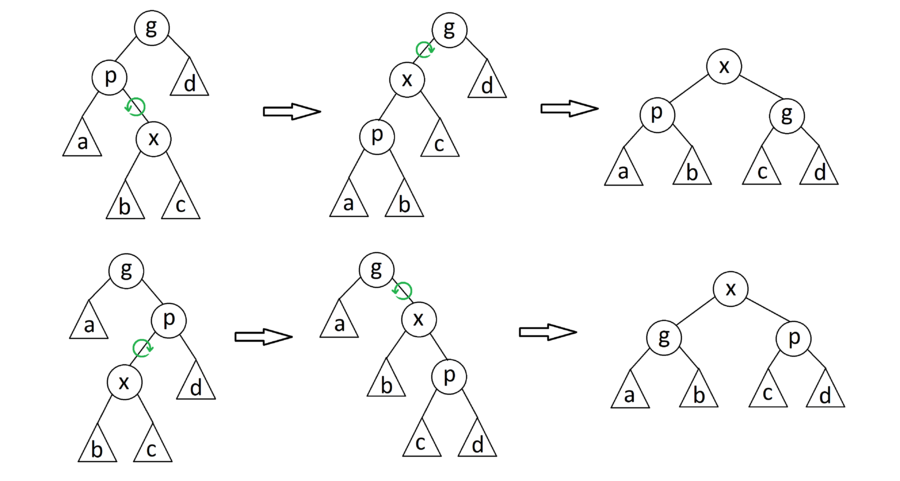
Проанализируем каждый шаг операции splay. Пусть [math]r'[/math] и [math]r[/math] — ранги вершин после шага и до него соответственно, [math]p[/math] — предок вершины [math]x[/math], а [math]g[/math] — предок [math]p[/math] (если есть). Разберём случаи в зависимости от типа шага: Zig. Поскольку выполнен один поворот, то амортизированное время выполнения шага [math]T = 1 + r'(x) + r'(p) - r(x) - r(p)[/math] (поскольку только у вершин [math]x[/math] и [math]p[/math] меняется ранг). Ранг вершины [math]p[/math] уменьшился, поэтому [math]T \le 1 + r'(x) - r(x)[/math]. Ранг вершины [math]x[/math] увеличился, поэтому [math]r'(x) - r(x) \ge 0[/math]. Следовательно, [math]T \le 1 + 3r'(x) - 3r(x)[/math]. Zig-zig. Выполнено два поворота, амортизированное время выполнения шага [math]T = 2 + r'(x) + r'(p) + r'(g) - r(p) - r(x) - r(g)[/math]. Поскольку после поворотов поддерево с корнем в [math]x[/math] будет содержать все вершины, которые были в поддереве с корнем в [math]g[/math] (и только их), поэтому [math]r'(x) = r(g)[/math]. Используя это равенство, получаем: [math]T = 2 + r'(p) + r'(g) - r(x) - r(p) \le 2 + r'(p) + r'(g) - 2r(x)[/math], поскольку [math]r(x) \le r(p)[/math]. Далее, так как [math]r'(p) \le r'(x)[/math], получаем, что [math]T \le 2 + r'(x) + r'(g) - 2r(x)[/math]. Мы утверждаем, что эта сумма не превосходит [math]3(r'(x) - r(x))[/math], то есть, что [math]r(x) + r'(g) - 2r'(x) \le -2[/math]. Преобразуем полученное выражение следующим образом: [math](r(x) - r'(x)) + (r'(g) - r'(x)) = \log_2 \frac{C(x)}{C'(x)} + \log_2 \frac{C'(g)}{C'(x)}[/math]. Из рисунка видно, что [math]C'(g) + C(x) \le C'(x)[/math], значит, сумма выражений под логарифмами не превосходит единицы. Далее, рассмотрим сумму логарифмов [math]\log_2 a + \log_2 b = \log_2 ab[/math]. При [math]a + b \le 1[/math] произведение [math]ab[/math] по неравенству между средними не превышает [math]1/4[/math]. А поскольку логарифм - функция возрастающая, то [math]\log_2 ab \le -2[/math], что и является требуемым неравенством. Zig-zag. Выполнено два поворота, амортизированное время выполнения шага [math]T = 2 + r'(x) + r'(p) + r'(g) - r(x) - r(p) - r(g)[/math]. Поскольку [math]r'(x) = r(g)[/math], то [math]T = 2 + r'(p) + r'(g) - r(x) - r(p)[/math]. Далее, так как [math]r(x) \le r(p)[/math], то [math]T \le 2 + r'(p) + r'(g) - 2r(x)[/math]. Мы утверждаем, что эта сумма не превосходит [math]2(r'(x) - r(x))[/math], то есть, что [math]r'(p) + r'(g) - 2r'(x) \le -2[/math]. Но, поскольку [math]r'(p) + r'(g) - 2r'(x) = \log_2 \frac{C'(p)}{C'(x)} + \log_2 \frac{C'(g)}{C'(x)} \le -2[/math] - аналогично доказанному ранее, что и требовалось доказать. Итого, получаем, что амортизированное время шага zig-zag не превосходит [math]2(r'(x) - r(x)) \le 3(r'(x) - r(x))[/math]. Поскольку за время выполнения операции splay выполняется не более одного шага типа zig, то суммарное время не будет превосходить [math]3r(t) - 3r(x) + 1[/math], поскольку утроенные ранги промежуточных вершин сокращаются (входят в сумму как с плюсом, так и с минусом). Тогда суммарное время работы splay [math]T_{splay} \le 3\log_2 N - 3\log_2 C(x) + 1 = O(\log_2 N)[/math], где [math]N[/math] - число элемнтов в дереве.

[math]\triangleleft[/math]

Статическая оптимальность сплей-дерева

Теорема:

Если к ключам [math]1[/math], ..., [math]n[/math], сложенным в сплей-дерево выполняется [math]m[/math] запросов, к [math]i[/math]-му ключу осуществляется [math]k_i[/math] запросов, где [math]k_i[/math] > 0, то суммарное время работы не превышает [math]O(m * H(p_1, p_2, .., p_n))[/math], где [math]p_i = k_i / m[/math], [math]H[/math] - шенноновская энтропия

Доказательство:

[math]\triangleright[/math]

Известно, что [math]H(p_1, p_2, .., p_n) = -c \cdot \displaystyle \sum_{i=1}^n (p_i \cdot \log_{2}p_i)[/math] — шенноновская энтропия. Пусть [math]s(x) = \displaystyle \sum_{y} w(y)[/math] — количество вершин в поддереве с корнем в [math]x[/math]. А [math]r(x) = \log_{2} s(x)[/math] — ранг вершины. Обозначим за [math]r[/math] корень [math]splay[/math]-дерева. Из предыдущей теоремы известно, что [math]a_{splay} \leqslant 1+3(r(r)-r(x))[/math] Пусть [math]w(x_i) = p_i =[/math] [math] {k_i \over m}[/math], тогда [math]k_i = p_i \cdot m[/math]. [math]m+3mr(r)-3 \displaystyle \sum_{i=1}^n k_ir(x_i) \leqslant m+3mr(r)-3 \displaystyle \sum_{i+1}^n k_i\log_{2}w(x_i) =[/math] [math] m+3mr(r)-3 \displaystyle \sum_{i=1}^n (p_i\cdot m\cdot \log_{2}p_i) = m(1+3r(r)-3 \displaystyle \sum_{i=1}^n p_i\log_{2}p_i) = (*)[/math] Так как вершина [math]r[/math] — корень [math]splay[/math]-дерева, то очевидно, что [math]s = \displaystyle \sum_{y} w(y) = 1[/math], следовательно [math]r(r) = \log_{2}s(r)=0[/math]. Поэтому [math](*) = m(1+H(p_1,...,p_n)) = O(mH(p_1,...,p_n))[/math], ч.т.д.

[math]\triangleleft[/math]

Теорема о близких запросах в сплей-дереве

Теорема (о близких запросах в сплей-дереве):

Пусть в сплей-дерево сложены ключи [math] 1, \dotsc, n [/math], зафиксируем один из ключей [math] f [/math], пусть выполняется [math] m [/math] запросов к ключам. Тогда суммарное время на запросы есть [math] \displaystyle O(n \log_{2} n + m + \sum_{i=1}^{m} \log_2 ( \lvert q_{i} - f \rvert + 1)) [/math], где [math] q_{i} [/math] — значение элемента, к которому обращаются в [math] i [/math]-ый запрос.

Доказательство:

[math]\triangleright[/math]

Для доказательства теоремы воспользуемся методом потенциалов: [math] a_{i} = t_{i} + \Phi_{i} - \Phi_{i-1} [/math]. По условию выполняется [math] m [/math] запросов, следовательно [math] T = \displaystyle \sum_{i=1}^{m} t_{i} = \sum_{i=1}^{m} \left(a_{i} + \Phi_{i-1} - \Phi_{i} \right) = \sum_{i=1}^{m} a_{i} + \sum_{i=1}^{m} \left( \Phi_{i-1} - \Phi_{i} \right) [/math] [math] (\ast) [/math]. Введем следующие обозначения: Весом узла с ключом [math] q [/math] будем называть величину [math] w(q) =\displaystyle \frac {1}{\left(\lvert q - f \rvert + 1 \right )^{2}} [/math]. Размером узла, содержащего ключ [math] q [/math], будем называть величину [math] s(q) = \displaystyle \sum_{y} w(y) [/math], где [math] y [/math] — узлы поддерева с корнем в [math] q [/math]. [math] r(q) = \log_{2}s(q) [/math] — ранг узла. Потенциал дерева после [math] i [/math]-го запроса обозначим как [math] \Phi_{i} = \displaystyle \sum_{q=1}^{n} r(q) = \displaystyle \sum_{q=1}^{n} \log_{2}s(q) [/math]. Пусть [math] W [/math] — вес дерева. Тогда [math] W = \displaystyle \sum_{q=1}^{n} w(q) = \sum_{q=1}^{n} \frac {1}{\left(\lvert q - f \rvert + 1 \right)^{2}} \leqslant 2 \cdot \sum_{q=1}^{+\infty} \frac {1}{ \left ( \lvert q - f \rvert + 1 \right)^{2}} = O(1) [/math]. Последнее верно, так как при фиксированном [math] f [/math], начиная с некоторого места, а именно [math] q = f [/math], ряд сходится. Из определения размера узла следует, что [math] w(q) \leqslant s(q) \leqslant W [/math]. Также заметим, что для любого [math] q [/math] от [math] 1 [/math] до [math] n [/math] верно, что [math] w(q) \geqslant \displaystyle \frac {1}{n^{2}} [/math], так как максимальное значение знаменателя в определении [math] w(q) [/math] достигается при [math] q = n [/math] и [math] f = 1 [/math] или наоборот. Тогда, воспользовавшись полученными оценками, найдем изменение потенциала сплей-дерева после [math] m [/math] запросов: [math]\displaystyle \sum_{i=1}^{m} \left( \Phi_{i-1} - \Phi_{i} \right) = \Phi_{0} - \Phi_{m} \leqslant \sum_{q=1}^{n} \log_{2} W - \sum_{q=1}^{n} \log_{2}w(q) = \sum_{q=1}^{n} \log_{2} \frac {W}{w(q)} [/math] [math] \displaystyle = O \Biggl(\sum_{q=1}^{n} \log_{2} n^{2}\Biggr) = [/math] [math] \displaystyle O\Biggl(2 \cdot\sum_{q=1}^{n} \log_{2} n\Biggr) = O\left(n \log_{2}n\right) [/math]. Обозначим за [math] t [/math] корень сплей-дерева. Тогда, воспользовавшись вышеуказанной леммой (можно показать, что она верна для любого фиксированного определения веса узла) получаем, что [math] \displaystyle a_{i} = 3 \cdot \left( r(t) - r(q_{i}) \right) + 1 = O\left(\log_{2} \frac{s(t)}{s\left(q_{i}\right)}\right) + 1 = O\left(\log_{2} \frac{W}{w(q_{i})}\right) + 1 = [/math] [math] O\left(\log_{2} \left(W \cdot \left(\lvert q_{i} - f \rvert + 1 \right)^{2} \right ) \right ) + 1 = O\left(\log_{2} \left(\lvert q_{i} - f \rvert + 1 \right) \right ) + 1 [/math]. Докажем, что данное определение потенциала удовлетворяет условию теоремы о методе потенциалов. Для любого [math] i [/math] верно, что [math] a_{i} = O(\log_{2}(n)) [/math], так как [math] \lvert q_{i} - f \rvert + 1 \leqslant n [/math], и [math] \Phi_{i} = O(n\log_{2}(n)) [/math], как было показано выше. Так как количество операций на запрос [math]k = O(n) [/math], то [math] a_{i} = O(f(k,n)) [/math] и [math] \Phi_{i} = O(kf(k,n)) [/math], где [math] f(k,n) [/math] — функция из теоремы о методе потенциалов, равная в данном случае [math] \log_{2}n [/math]. Следовательно потенциал удовлетворяет условию теоремы. Тогда, подставляя найденные значения в формулу [math] (\ast) [/math], получаем, что [math]T=\displaystyle \sum_{i=1}^{m} \left ( O \left( \log_{2} \left ( \lvert q_{i} - f \rvert + 1 \right) \right) + 1 \right ) + O\left ( n \log_{2} n \right) = [/math] [math] \displaystyle O \left (n \log_{2} n + m + \displaystyle \sum_{i=1}^{m} \log_{2} \left( \lvert q_{i} - f \rvert + 1 \right) \right)[/math]. Данная теорема показывает, что сплей-деревья поддерживают достаточно эффективный доступ к ключам, которые находятся близко к какому-то фиксированному ключу.

[math]\triangleleft[/math]

Splay-деревья по неявному ключу

Splay-дерево по неявному ключу полностью аналогично декартову дереву по неявному ключу, неявным ключом также будет количество элементов дерева, меньших данного. Аналогично, будем хранить вспомогательную величину [math]C(x)[/math] — количество вершин в поддереве. К операциям, которые уже были представлены в декартовом дереве, добавляется splay, но пересчет [math]C(x)[/math] в ней тривиален, так как мы точно знаем, куда перемещаются изменяемые поддеревья.

Литература

• Википедия - Splay tree
• Sleator, Daniel D.; Tarjan, Robert E."Self-Adjusting Binary Search Trees"