Алгоритм Ландау-Вишкина (k несовпадений)
Содержание
Постановка задачи
Дано число текст и образец , . Требуется найти все подстроки текста длины , с не более чем несовпадающими символами.
Алгоритм
При анализе используется двумерный массив несовпадений текста , содержащий информацию о несовпадениях текста с образцом. По завершении анализа в его -й строке содержатся позиции в первых несовпадений между строками и . Таким образом, если , то , и это -е несовпадение между и , считая слева направо. Если число несовпадений с подстрокой меньше , то, начиная с , элементы -й строки равны значению по умолчанию .
Заметим, если , то подстрока отличается от образца не более, чем на символов, и, таким образом, является решением задачи.
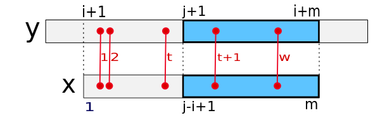
Затем образец сканируется параллельно с текстом слева на права по одному символу за раз. На итерации с образцом сравнивается подстрока . - обозначим самую правую позицию в тексте, достигнутую за предыдущие итерации, то есть является максимальным из чисел , где . Если , в присваивается результат работы , которая находит количество несовпадений между и . Если не превышает , вызывается процедура , которая сравнивает подстроки и . Переменная будет рассмотренна ниже.
|
tm[0...n-m][1...k+1] = m+1 // инициализация
r = 0
j = 0
for i = 0 to n - m
b = 0
if i < j
b = merge(i, r, j)
if b < k + 1
r = i
extend(i, j, b)
|
extend
Рассмотрим процедуру подробнее. Она сравнивает подстроки и , в случае несовпадения увеличивается и таблица текстовых несовпадений обновляется. Это происходит пока либо не будет найдено несовпадений (учитывая несовпадения, которые были найдены раньше на -ой итерации), либо не будет достигнуто с не больше чем несовпадениями, то есть найдено вхождение образца, начинающееся с .
|
extend(i, j, b)
while (b < k + 1) and (j - i < m)
j++
if y[j] != x[j-1]
b++
tm[i][b] = j - i
|
merge
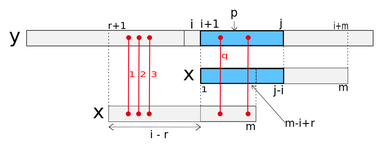
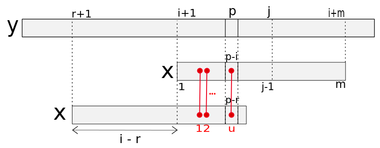
Рассмотрим процедуру подробнее. Она находит количество несовпадений между и и устанавливает b равным найденному числу, при этом используется полученая ранее информация. Введем - это строка таблицы несовпадений, в которой есть информация о несовпадениях, полученных при совмещении начала образца и . содержит текущий номер самой правой из проверенных на настоящий момент позиций текста. Поэтому при обработки построки начинающейся с , можно учитывать информацию в -ой строке , которая содержит информацию о сопоставлении образца с . Подходящими значениями из таблицы несовпадений являются, таким образом, , где – это наименьшее из целых чисел, для которых . Однако, следует учитывать тот факт, что эти несовпадения соответствуют началу образца, выравниваемому с , в то время как текущая позиция образца выровнена с – разница в мест.
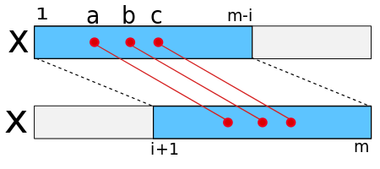
Также в алгоритме используется двумерный массив несовпадений образца , генерируемой на стадии предварительной обработки образца. В нем содержатся позиции несовпадения образца с самим собой при различных сдвигах, аналогично , то есть в -ой строке содержитатся позиции внутри первых несовпадений между подстроками и . Таким образом, если , то , и это -е несовпадение между и слева направо. Если число несовпадений между этими строками меньше , то, начиная с , элементы -й строки равны , значению по умолчанию.
Таким образом, для интерес представляет строка таблицы несовпадений, причем используются значения , где – самое правое несовпадение в , такое, что , так как требуются только несовпадения в подстроке .
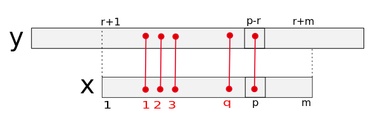
Чтобы использовать упомянутую информацию в процедуре , рассмотрим в тексте позицию , находящуюся в диапазоне, . Рассмотрим следующие условия для позиции :
Условие A: когда символы и совмещены, позиция в тексте соответствует предварительно выявленному несовпадению между образцом и текстом, то есть , и это несовпадение номер , где , то есть .
Условие B: для двух копий образца, со сдвигом относительно друг друга , совмещенных с текстом так, что их начальные символы лежат, соответственно, над и , позиция соответствует несовпадению между двумя шаблонами, то есть . Это -е несовпадение при этом сдвиге, где , то есть = .
Пример
Пусть , , .
| tm | 1 | 2 | 3 | x[1..m] | y[i+1..i+m] |
| 0 | 2 | 3 | 4 | tram | thet |
| 1 | 1 | 2 | 3 | tram | hetr |
| 2 | 1 | 2 | 3 | tram | etri |
| 3 | 3 | 4 | 5 | tram | trip |
| 4 | 1 | 2 | 3 | tram | ripp |
| 5 | 1 | 2 | 3 | tram | ippe |
| 6 | 1 | 2 | 3 | tram | pped |
| 7 | 1 | 2 | 3 | tram | pedt |
| 8 | 1 | 2 | 3 | tram | edtr |
| 9 | 1 | 2 | 3 | tram | dtra |
| 10 | 4 | 5 | 5 | tram | trap |
| tm | 1 | 2 | 3 | 4 | 5 | x[1..m-i] | x[i+1..m] |
| 1 | 1 | 2 | 3 | 5 | 5 | tra | ram |
| 2 | 1 | 2 | 5 | 5 | 5 | tr | am |
| 3 | 1 | 5 | 5 | 5 | 5 | t | m |