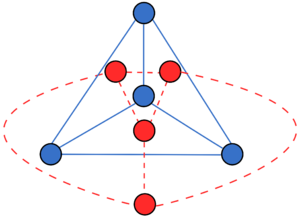
Двойственный граф планарного графа

Эта статья находится в разработке!

Определение:

Граф G′ называется двойственным к планарному графу G, если:

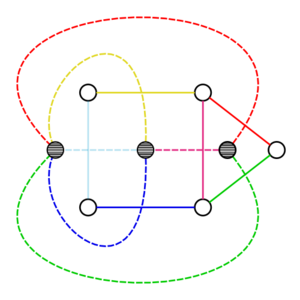
1. Вершины G′ соответствуют граням G
2. Между двумя вершинами в G′ есть ребро тогда и только тогда, когда соответствующие грани в G имеют общее ребро

Граф (белые вершины) и двойственный ему (полосатые вершины).

«…Для данного плоского графа G его двойственный граф G′ строится следующим образом: поместим в каждую область G (включая внешнюю) по одной вершине графа G′ и, если две области имеют общее ребро x, соединим помещенные в них вершины ребром x′, пересекающим только x. В результате всегда получится плоский псевдограф. Ясно, что G′ имеет петлю тогда и только тогда, когда в G есть концевая вершина; G′ имеет кратные рёбра тогда и только тогда, когда две области графа G содержат по крайней мере два общих ребра. Таким образом, двусвязный плоский граф имеет всегда в качестве двойственного или граф или мультиграф, в то время как двойственный граф трёхсвязного плоского графа всегда представляет собой граф. Другими примерами двойственных графов являются платоновы графы: тетраэдр — самодвойственный граф, куб и октаэдр — двойственные, так же как додекаэдр и икосаэдр…».

В верхнем двойственном графе есть вершина степени 6, а в нижнем — нет. Следовательно, они не изоморфны.

Свойства

Дерево и двойственный к нему «цветок».‎

• Если G′ — двойственный к двусвязному графу G, то G — двойственный к G′
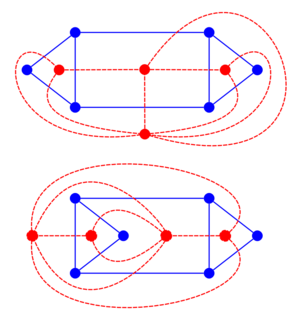
• У одного и того же графа может быть несколько двойственных, в зависимости от конкретной укладки (см. картинку)
• Поскольку любой трёхсвязный планарный граф допускает только одну укладку на сфере, у него должен быть единственный двойственный граф
• Мост переходит в петлю, а петля — в мост
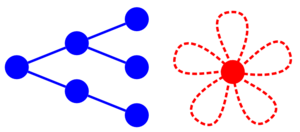
• Мультиграф, двойственный к дереву, — цветок

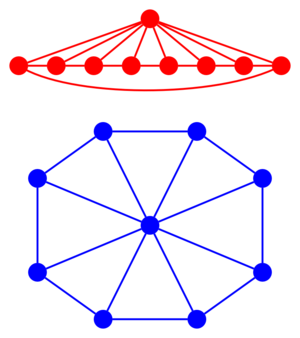
Самодвойственные графы

Определение:

Планарный граф называется самодвойственным, если он изоморфен своему двойственному графу.

Колесо и колесо.

[math]K_4[/math] (он же кольцо).

Утверждение:

[math]K_1[/math] и [math]K_4[/math] — самодвойственные графы. Среди полных графов других самодвойственных нет.

[math]\triangleright[/math]

Проверить, что [math]K_1[/math] и [math]K_4[/math] полны и самодвойственны несложно. Докажем, что других нет.
Поскольку грани графа переходят в рёбра, количество рёбер и граней в исходном графе должно совпадать, т.е. [math]V = F[/math].
Подставив в формулу Эйлера имеем: [math]2V = E + 2 \Leftrightarrow V = \frac{E}{2} + 1[/math].
В полном графе [math]E = \frac{V \dot (V - 1)}{2}[/math].
Получаем квадратное уравнение: [math]V^2 - 5V + 4 = 0[/math].
Его решения: [math]V_1 = 1[/math] и [math]V_2 = 4[/math].
Таким образом, чтобы полный граф был самодвойственным, в нём должна быть ровно одна или четыре вершины.

[math]\triangleleft[/math]

Утверждение:

Все колёса самодвойственны.

[math]\triangleright[/math]

Это утверждение очевидно. Достаточно посмотреть на два варианта укладки колеса (вершина с большой степенью внутри или вершина с большой степенью снаружи) и убедиться в том, что они двойственны друг другу.

[math]\triangleleft[/math]