Straight skeleton
Существует целый класс структур типа , которые описывают базовые топологические свойства объектов. Структура была придумала Oswin Aichholzer. Она используются в различных практических задачах (проектирование крыш для зданий) и для доказательства некоторых теорем[1].
Содержание
Топологические свойства
| Определение: |
| Straight skeleton (Angular Bisector Network, ABN) полигона без самопересечений называется планарный граф, определяющий разбиение полигона на регионы, границами которых являются стороны полигона, биссектрисы углов и отрезки, соединяющие вершины straight skeleton, образовавшиеся в результате сжатия полигона. |
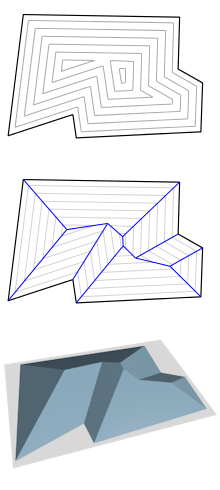
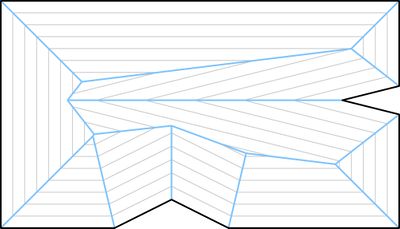
Опишем подробней, как получается такое разбиение. Мы можем представить, будто все стороны прямоугольника параллельно двигаются внутрь с одинаковой постоянной скоростью, то есть многоугольник как бы сжимается внутрь. Тогда вершины будут двигаться вдоль биссектрис , а точки пересечения биссектрис будут соединять совпавшие участки сторон прямоугольника в конце движения. В каждый момент времени от начала движения рёбер мы получаем слоистую структуру (рис 1.). На рис. 2 синим цветом выделен — множество отрезков, образованных точками пересечения при движении сторон полигона. Чем-то структура похожа на строение крыши в домах (рис. 3). И для решения этой задачи как раз и может применяться: по стенам здания необходимо спроектировать его крышу.
Процесса стягивания многоугольника продолжается до тех пор, пока происходят его топологические изменения, то есть меняется число вершин в стянутом многоугольнике, и таким образом появляются новые вершины дерева . Существуют два типа изменений, в ходе которых образуются новые вершины дерева:
- — данное изменение происходит, когда сторона многоугольника полностью стягивается, делая соседние стороны инцидентными.
- происходит, когда ребро разбивается на два новых ребра, исходящих из точки преломления старого. Такое событие происходит на биссектрисе вогнутой вершины многоугольника. И тогда стягиваемая многоугольником область разбивается на две непересекающиеся многоугольные области.
На рисунке ы изображён красным кругом, а ы — чёрным прямоугольником.
Таким образом, ы соответствуют внутренним вершинам , гранями являются области многоугольника, заметаемые сторонами многоугольника в процессе стягивания, дуги соединяют либо две внутренние вершины либо внутреннюю вершину с листом — вершиной многоугольника.
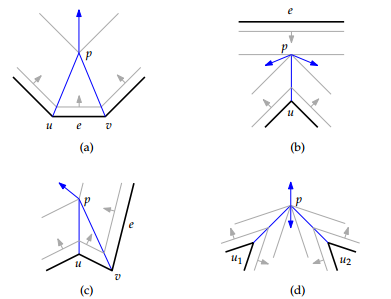
Стоит также отметить, что в общем случае ы могут быть нетривиальными. На рисунке ниже в случае в вершине совпали из вершины и ребра , а в случае совпали два а вершин и . Случаи и — простые и ы.
Свойства Straight skeleton
Из процесса построения следует, что он является планарным графом. Ранее уже упоминалось, что он также является деревом. Будем обозначать простого полигона без самопересечений , в котором вершин, как . Тогда справедливы следующие леммы:
| Лемма (1): |
является деревом, содержит граней, не более внутренние вершины и не более рёбер. |
| Доказательство: |
|
Каждая грань начинает образовываться во время стягивания ребра , и даже если на ребре произошёл , сама грань не могла разделиться. Построение грани завершается, когда ребро полностью стягивается. И это ребро дальше не может появиться снова, поэтому граней в столько, сколько сторон в многоугольнике, то есть ровно . То, что является деревом, легко доказывается по индукции. База верна, когда внутренняя вершина всего одна. Тогда у листьями будут вершины многоугольника. Такой граф очевидным образом будет деревом. Если в внутренних вершин, то рассмотрим самый первый . Он закончился в какой-то внутренней вершине , у неё есть смежные листья — вершины, инцидентные этому ребру, — и из неё достижимы другие ы, с не более чем внутренними вершинами, и они являются деревьями по предположению индукцию. Тогда получаем, что для вершин тоже будет деревом. Внутренние вершины в имеют степень не меньше — простой перебор всех случаев ов (степень будет больше, если в одной вершине совпало несколько событий). Так как имеет листьев, то внутренних вершин будет не больше , а так как является деревом, то рёбер у него будет не более . |
Замечание: если мы рассмотрим в какой-то момент времени, то он вполне может содержать циклы (это видно на одном из рисунков выше). Однако его конечная структура будет деревом.
Алгоритм с изпользованием SLAV
Далее будет описан алгоритм, придуманный Petr Felkel, который строит за время , где — общее число вершин в полигоне, — число вогнутых вершин в полигоне. Немного модифицированный этот алгоритм используется в открытой библиотеке вычислительной геометрии CGAL[2]. Однако этот алгоритм всё равно ещё достаточно медленный. В реальной жизни используют его модификации или более сложные алгоритмы.
Сначала алгоритм будет рассмотрен на простом случае — выпуклом многоугольнике, — а потом на невыпуклом многоугольнике.
Выпуклый полигон
В случае выпуклого многоугольника возникают только ы по определению. Поэтому просто алгоритм можно описать следующим образом: найдём точки пересечения биссектрис многоугольника для каждой вершины со всеми соседними вершинами, возьмём такую точку, в которой произойдёт самый первый , добавим полученную вершину в , соеденим её с вершинами ребра, которое исчезло в процессе текущего а, а потом перестроим полигон, создав новую вершину и подвинув все остальные вдоль биссектрис на одинаковое расстояние. Будем продолжать этот процесс до тех пор, пока многоугольник не превратится в треугольник.
Теперь реализуем этот алгоритм более эффективно. Для этого мы будем использовать специальную структуру данных — (set of circular lists of active vertices). Эта структура хранит цикл всех вершин для внешней грани, а так же цикл для каждой дыры многоугольника и для всех многоугольников, возникающих в процессе построения . В данном случае у нас будет просто — циклический список всех вершин многоугольника.
Далее считаем, что полигон представлен рёбрами вдоль движения по контуру полигона против часовой стрелки. Алгоритм будет следующим:
- Инициализация
- (a) Поместим все вершины многоугольника в двусвязный циклический список в порядке обхода вдоль контура.
Невыпуклый полигон
Невыпуклый полигон с дырами
Алгоритм построения с помощью Motorcycle graph
Рассмотрим алгоритм построения на основе мотографов.
TODO: Алгоритм на мотографах
Другие алгоритмы
Существует простой в понимании и реализации алгоритм для построения на основе триангуляции, который работает за время [3]. Aichholzer смог обобщить этот алгоритм для построения произвольного планарного графа[4]. Также автором в его оригинальной статье был представлен алгоритм построения данной структуры, базирующийся на понятии волнового фронта (англ. wavefront). Этот алгоритм может быть реализован за время с использованием памяти либо с использованием приоритетной очереди за время и памяти[5]. Известен алгоритм построения для монотонных полигонов за время с использованием памяти[6].
В данном конспект был (P.S. точнее, ещё будет) представлен алгоритм на основе мотографов, который придумали Stefan Huber и Martin Held. Они говорят, что даже смогли реализовать этот алгоритм, но код нигде не выкладывали.
Примечания
- ↑ Wikipedia — Fold-and-cut theorem
- ↑ Stepan Obdrazalek, "The Angular bisector network Implementation and the CGAL library"
- ↑ Stefan Huber, Martin Held, "Straight Skeletons and their Relation to Triangulations"
- ↑ Oswin Aichholzer, Franz Aurenhammera, "Straight Skeletons for General Polygonal Figures in the Plane"
- ↑ Oswin Aichholzer, Franz Aurenhammera, "A Novel Type of Skeleton for Polygons"
- ↑ Therese Biedl, Martin Held, Stefan Huber, Dominik Kaaser, Peter Palfrader, "Straight Skeletons of Monotone Polygons"