Триангуляция Делоне на сфере

Определение

Определение:

Триангуляция — набор непересекающихся отрезков, соединениющий заданный набор точек так, что добавление новых отрезков невозможно без пересечения уже имеющихся.

Определение:

Отрезок — кратчайшее расстояние от точки до точки на заданной поверхности.

Определение:

Симплекс(англ. simplex) — геометрическая фигура, являющаяся n-мерным обобщением треугольника.

Определение:

Триангуляция — разбиение геометрической фигуры на симплексы.

Определение:

Критерий Делоне: при построении плоскости через три точки, образующие треугольник, все остальные точки лежат ниже этой плоскости.

Определение:

Локальный критерий Делоне: при построении плоскости через три точки, образующие треугольник, противолежащие сторонам треугольника вершины соседей лежат ниже этой плоскости.

Определение:

Критерий Делоне для ребра: через ребро можно провести плоскость так, что все точки будут лежать ниже этой плоскости.

Определение:

Локальный критерий Делоне для ребра: через ребро можно провести плоскость так, что вершины, противолежащие этому ребру, будут лежать ниже этой плоскости

Существования триангуляции Делоне

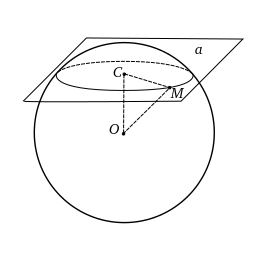
Лемма (1):

Сечение сферы плоскостью есть круг, а основание перпендикуляра проведенного из центра шара к пересекаемой плоскости есть центр круга, полученного в сечении.

Доказательство:

[math]\triangleright[/math]

Пусть плоскость [math]\alpha[/math] пересекает сферу. Из центра [math]O[/math] опустим перпендикуляр [math]OC[/math] на плоскость [math]\alpha[/math]. Соединим произвольную точку [math]M[/math] линии пересения плоскости [math]\alpha[/math] со сферой с точками [math]O[/math] и [math]C[/math]. Так как [math]OC[/math] ⊥ [math]\alpha[/math], то [math]OC[/math] ⊥ [math]CM[/math]. В прямоугольном треугольнике [math]OCM CM2 = OM2 - OC2[/math]. Т.к. [math]OM[/math] и [math]OC[/math] - величины постоянные, то и [math]CM[/math] - величина постоянная. Таким образом все точки линии пересечения плоскости [math]\alpha[/math] и сферы равноудалены от точки [math]C[/math], поэтому эта линия пересечения является окружностью с центром в точке [math]C[/math] и радиусом [math]r = CM[/math].

[math]\triangleleft[/math]