Теорема Вагнера
| НЕТ ВОЙНЕ |
|
24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России |
| Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению. |
| meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки. |
Вагнер опубликовал теорему в 1937, после публикации в 1930 теоремы Куратовского, согласно которой граф планарен тогда и только тогда, когда он не содержит подграфов гомеоморфных и . Теорема Куратовского сильнее теоремы Вагнера — гомеоморфный подграф может быть преобразован в минор того же типа путём стягивания всех, кроме одного, рёбер в каждом пути, полученном при разбиении ребра путем добавления вершины, а вот обратное преобразование из минора в гомеоморфный подграф того же типа не всегда возможно.
Содержание
| Определение: |
| Минором графа (англ. Graph minor) будем называть граф , если может быть образован из удалением рёбер и вершин или стягиванием рёбер. |
Миноры графов часто изучаются в более общем контексте миноров графовых матроидов. В этом контексте обычно полагается, что графы связны, могут иметь петли и кратные рёбра (то есть, рассматриваются псевдографы, а не простые графы). Стягивание петли и удаление разрезающего ребра запрещены. При таком подходе удаление ребра оставляет ранг графа неизменным, а стягивание ребра всегда уменьшает ранг на единицу.
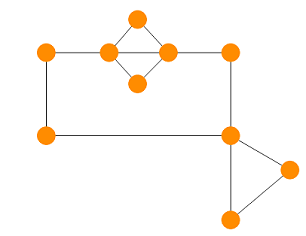
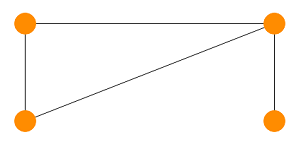
Пример
В следующем примере граф является минором графа :
Теорема
| Теорема: |
Граф планарен тогда и только тогда, когда его миноры не содержат ни ни . |
| Доказательство: |
|
Иначе говоря в соответствии с теоремой Понтрягина-Куратовского, теорему можно переформулировать: « В графе есть миноры содержащие или тогда и только тогда, когда существует подграф гомеоморфный или »
Разделим доказательство на две части
Доказательство первой части
В силу определения минора, если в существует минор содержащий ,значит существуют множества вершин , , , , , попарно не пересекающиеся, образующие индуцированный связанный подграф , такие что для каждого и существует и и , принадлежит множеству ребер исходного графа. Следовательно для каждого существует поддерево в , у которого три листа , , , а все остальные вершины подграфа принадлежат . Ситуация с симметрична. Доказательство второй части
В силу определения минора, если в существует минор содержащий ,значит существуют множества вершин попарно не пересекающиеся, образующие индуцированный связанный подграф , такие что для всех существует и , такие что ( ) принадлежит множеству ребер исходного графа. Следовательно для любого существует поддерево в с четырьмя листьями, по одному листу в каждом и с остальными вершинами внутри .
Такое «обрезание» приведет к тому что будут иметь по три вершины, каждая содержится в таком подграфе, что она окрашено в другой цвет чем остальные вершины. Граф сформированный из красных и синих вершин вместе с оставшимися ребрами изоморфен .
|
См. также
Источники информации
- Graph minor — Wikipedia
- Geir Agnarsson, Raymond Greenlaw. Graph Theory: Modeling, Applications and Algorithms, 2006 — глава 7.5 стр. 210