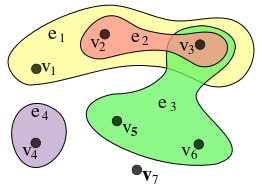
Гиперграфы
В математике гиперграф - это обобщение графа, у которого ребра могут соединять любое количество вершин. Более формально, гиперграф - это пара , где - множество элементов называемых узлами или вершинами, и - не пустое подмножество называемых гиперребрами или просто ребрами.
В то время, как ребра графа соединяют две пары вершин, гиперребра - произвольные множества вершин, которые могут содержать любое количество вершин. Однако, очень часто рассматривают гиперграфы с гиперребрами одинаковой мощности ; - равномерный гиперграф - это такой гиперграф, у которого все гиперребра имеют размер k. (Другими словами, такой гиперграф множество подмножеств, которые содержат k вершин). Так например, - равномерный гиперграф - обычный граф.
Стоит заметить, что обычный граф является частным случаем гиперграфа, где каждое ребро имеет мощность .
Определения
Так как множество гиперребер может быть любой мощности, существуют несколько понятий подграфа гиперграфа, называемых подгиперграфами, частичные гиперграфы и разрез гиперграфов. Пусть - гиперграф содержащий множество вершин и множество ребер , где и множества индексов вершин и ребер соответсвенно.
Подгиперграфом называют гиперграф с некоторым множеством удаленных вершин. Формально, подгиперграф , индуцированный подмножеством множества , который определен как
Частичным гипергафом называется гиперграф, с множеством удаленных ребер. Данное подмножество множества индексов ребер, частичный граф сгенерирован с помощью , т.е
Пусть дано множество , разрезом гиперграфа называют такой частичный гиперграф
Двойственным гиперграфом * к называют такой гиперграф, в котором поменяны местами вершины и ребра таким образом, что вершины определяются как и ребра определяются как , где
Когда операция равенства определена, как показано ниже, операция взятия двойственного гиперграфа выглядит следующим образом
Связный граф с тем же множеством вершин, что и у связного гиперграфа называется «принимающим» графом для , если каждое гиперребро включает связный подграф в . Для несвязного гиперграфа , является «принимающим», если существует биекция между связными компонентами и , так что каждая связная компонента ' графа является принимающей для соответствующего '.
Изоморфность и эквивалентсность
Гиперграф изоморфен гиперграфу , если существует биекция : -> и перестановка множества такая, что = Тогда биекция называется изоморфизмом гиперграфов. Стоит отметить, что тогда и только тогда, когда *
Ацикличность
В отличие от обычных неориентированных графов, для которых существует только одно понятие ацикличности, существует множество неэквивалентных определений ацикличности гиперграфов.
Первое определение ацикличности для гиперграфов было дано Клаудом Бержем: гиперграф называется ацикличным по Бержу, если инцидентный ему граф ацикличный. Это определение достаточно ограничено. Например, если гиперграф имеет какую-то пару вершин и какую-то пару гиперребер , таких что и , тогда имеет место цикл по Бержу. Цикличность по Бержу может быть найдена за линейное время с помощью исследования инцидентности гиперграфа.
Также мы можем определить более слабое определение ацикличности гиперграфа, называемое - ацикличность. Это понятие ацикличности эквивалентно определению гиперграфа, который является конформальным(т.е. каждая клика исходного графа покрыта каким-то гиперребром), и при этом исходный граф является хордальным ; это также эквивалентно сводимости пустого графа через GYO алгоритм(более известный как алгоритм Грэхема), повторяющийся процесс, который удаляет гиперребра с использованием главного определения "ухо графа". В области теории баз данных известно, что схема баз данных обладает некоторыми желательными свойствами, если ее основной граф является - ациклическим. - ацикличность гиперграфа также может быть найдена за линейное время.
Стоит отметить, что - ацикличность графа имеет некоторое нелогичное свойство, а именно, что при добавлении к - цикличному графу гиперребер гиперграф может стать - ацикличным. Например, добавление гиперребра, которое содержит все вершина гиперграфа, всегда будет давать - ацикличность графа. Частично мотивированным этим недостатком, Рональд Феджин определил более сильные понятия - - ацикличность и - ацикличность. Можно констатировать - ацикличность как требование, чтобы все подгиперграфы исходного гиперграфа были - ацикличными, что ээквивалентно выше упомянотому определению Грэхема. Понятие - ацикличности имеет более ограниченное определение, которое эквивалентно несколькими желательными свойствами схем баз данных и связана с диаграммами Бахмена. <tex<\beta</tex> - ацикличность и - ацикличность может быть найдена за полиномиальное время.
Матрица инцидентности
Пусть и . Каждый гиперграф имеет инцидентную матрицу , где
Транспонированная матрица инцидентной матрицы определяет гиперграф называемая двойственной к , где явялется -ым элементом множества и является -ым элементом множества подмножества . Для и если, и только если .