Гиперграфы
| Определение: |
| Гиперграфом (англ. hypergraph) называют такую пару , где множество вершин, а семейство подмножеств X, называемых гиперребрами (англ. hyperedges) |
Обычные графы, у которых ребра могут соединять только две вершины, являются частным случаем гиперграфа, у которых все гиперребра содержат только две вершины.
Основные понятия гиперграфов
| Определение: |
Путем (англ. path, смотри также путь в обычном графе) между двумя гиперребрами и гиперграфа называется последовательность гиперребер таких что :
|
| Определение: |
| Гиперграф называется связным (англ. connected) тогда и только тогда, когда существует путь между каждой парой гиперребер. |
Пусть - набор гиперребер, и - элементы и .
| Определение: |
| называется сочленением (англ. articulation) , если при его удалении из всех гиперребер , множество разрывается. |
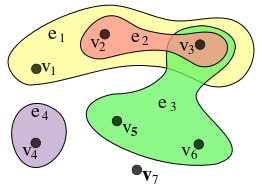
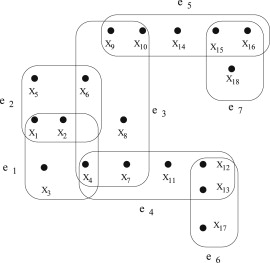
На Рис.2 является сочленением .
Матрица инцидентности
Пусть дан гиперграф , где и . Любой гиперграф может задаваться матрицей инцидентности (смотри матрицу инцидентности в обычном графе) размером , где
Так например, для гиперграфа на рис.1 мы имеем такую матрицу инцидентности
Ацикличность гиперграфа
| Определение: |
Циклом в называется последовательность гиперребер удовлетворяющим следующим свойствам:
|
Для определения ацикличного гиперграфа введем определение уха гиперграфа, а также редукцию GYO(Graham-Yu-Ozsoyoglu).
| Определение: |
Ухом (англ. ear) гиперграфа называется такое гиперребро , что его вершины можно разделить на две группы:
|
| Определение: |
Определение редукции GYO (англ. GYO reduction) содержит всего два шага:
|
То есть, мы удаляем вершины которые содержатся в ухе, и ни в каком более гиперребре. Затем удаляем гиперребра, оставляя другие вершины.
| Утверждение: |
Если гиперграф сводится к пустому с помощью редукции GYO, тогда он ацикличный. |
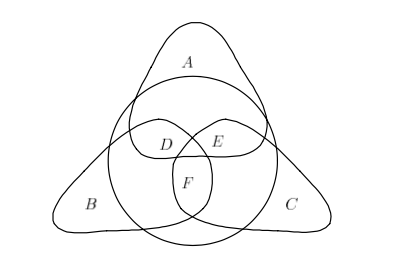
С помощью редукции GYO удаляются вершины A, B и C (т.к они содержатся только в одном своем гиперребре), а затем удаляем оставшиеся внутренние гиперребра.