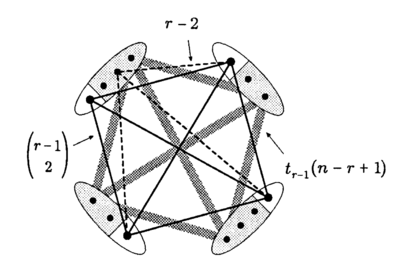
Теорема Турана об экстремальном графе

Теорема Турана

Теорема Ту́рана (англ. Turán's theorem) — классическая теорема экстремальной теории графов. Она послужила образцом для большого количества подобных теорем, которые изучают некоторые глобальные параметры, такие как хроматическое число, относительно присутствия тех или иных подструктур.

Впервые задачу сформулировал Пал Туран в 1941 году.

Определение:

[math]ex(n, K^r)[/math] — максимальное количество ребер в графе на [math]n[/math] вершинах, которые не содержит [math]K^r[/math] как подграф.

Определение:

Граф Турана [math]T^{r-1}(n)[/math] — единственный полный [math](r - 1)[/math]-дольный полный граф на [math]n \gt r-1[/math] вершинах, доли которого по мощности не отличаются более чем на 1. Если [math]n \leqslant r - 1[/math], то [math]T^{r-1}(n) = K^n[/math].

Пример графа Турана

Определение:

[math] t_{r-1}(n) [/math] — количество ребер в [math]T^{r-1}(n)[/math].

Теорема:

Для всех целых чисел [math]r[/math], [math]n[/math], где [math]r \gt 1[/math], любой граф [math]G \nsubseteq K^r[/math] с [math]n[/math] вершинами и [math]ex(n, K^r)[/math] ребрами есть [math]T^{r-1}(n)[/math].

Доказательство:

[math]\triangleright[/math]

Шаг индукции

[math]\triangleleft[/math]

Источники информации

Дистель, Рейнград. Теория графов: Пер. с англ. — Новосибирск: Изд-во Ин-та математики, 2002. — 166-170 стр. — ISBN 5-86134-101-X.