| Задача: |
| Дана перестановка [math]\pi[/math] множества [math]~\{1, 2,~\dots,~n\}[/math]. Требуется найти НВП [math]\pi[/math] за [math]O(n\operatorname{log}\operatorname{log}k)[/math], где [math]k[/math] — длина НВП. |
Алгоритм за O(n log log n)
Нахождение длины НВП
Основная идея
Пусть [math]\{\pi_1,\pi_2,~\dots,~\pi_n\}[/math] — входная перестановка.
Будем последовательно обрабатывать элементы в порядке [math]\pi_1, \pi_2,~\dots,~\pi_n\colon[/math]
Для каждой длины [math]l = 1, 2,~\dots,~n[/math] предполагаемой НВП находим наименьший элемент, который может быть последним в возрастающей подпоследовательности длины [math]l[/math] и запишем его в массив [math]B_l[/math]. Будем называть его наилучшим элементом для длины [math]l[/math].
- Если [math]\pi_i[/math] больше каждого элемента [math]B[/math], вычисленного для подпоследовательности [math]\pi_1, \pi_2,~\dots~,\pi_{i-1}[/math], тогда с ним можно сделать возрастающую подпоследовательность максимальной длины из уже рассмотренных, в которой он будет последним элементом. Значит, записываем его в конец [math]B[/math].
- Иначе [math]\pi_i[/math] будет наилучшим элементом для уже существующей длины, тогда мы находим наименьшее [math]k\colon B_k \gt \pi_i[/math] и заменяем [math]B_k[/math] элементом [math]\pi_i[/math].
Следует отметить, что полученный массив также образует возрастающую последовательность, на котором мы должны выполнять операции [math]\mathrm{insert}, \mathrm{next}, \mathrm{delete}[/math], соответственно целесообразно использовать приоритетную очередь, реализованную через Дерево ван Эмде Боаса. Так как данная структура данных производит описанные операции за [math]O(\operatorname{log} k)[/math], где k — количество бит чисел, которые позволяет хранить дерево, то полученный алгоритм работает за [math]O(n\operatorname{log}\operatorname{log} n)[/math], потому что все элементы последовательности не превосходят n.
Доказательство оптимальности
| Утверждение: |
Пусть [math]S=\{\pi_1,\pi_2,~\dots,~\pi_n\}[/math] — входная перестановка. В результате описанного алгоритма размер массива [math]B[/math] равен длине НВП последовательности [math]S[/math] |
| [math]\triangleright[/math] |
|
Докажем, что перед обработкой и после обработки элемента последовательности алгоритмом сохраняется инвариант, что в массиве [math]B[/math] хранятся наилучшие элементы для каждой возможной длины возрастающих подпоследовательностей обработанной последовательности.
- Пусть перед обработкой элемента [math]\pi_i[/math] соблюдается описанное выражение инварианта.
- Если [math]\pi_i[/math] больше каждого элемента [math]B[/math], вычисленного для последовательности [math]S_{i-1}=\{\pi_1,\pi_2,~\dots,~\pi_{i-1}\}[/math], то он не может обновить любой из наилучших элементов, вычисленных ранее. С [math]\pi_i[/math] можно составить возрастающую последовательность длины [math]l+1[/math], где [math]l[/math] — длина НВП последовательности [math]S_{i-1}[/math], добавив [math]\pi_i[/math] в конец этой НВП. Значит, [math]\pi_i[/math] — наилучший элемент длины [math]l+1[/math]. По предположению, размер [math]B[/math] равен длине НВП последовательности [math]S_{i-1}[/math], потому что в [math]B[/math] хранятся наилучшие элементы всех возможных длин возрастающих подпоследовательностей [math]S_{i-1}[/math]. Тогда, добавив в конец очереди [math]B[/math] элемент [math]\pi_i[/math], инвариант будет сохраняться.
- Иначе [math]\pi_i[/math] будет наилучшим элементом для уже существующей длины. Заметим, что [math]\pi_i[/math] может обновить только один элемент. В обратном случае, если [math]\exists l_1,l_2\colon l_2\gt l_1[/math], для которых [math]\pi_i[/math] может быть наилучшим элементом, то существует такая подпоследовательность длины [math]l_2[/math], в которой [math]\pi_i[/math] является наибольшим элементом, но из этой последовательности можно составить подпоследовательность длины [math]l_1[/math], в которой наибольший элемент меньше [math]\pi_i[/math], что противоречит предположению. Таким образом, [math]\pi_i[/math] может обновить только наименьшее [math]k\colon B_k \gt \pi_i[/math]. Тогда, заменив [math]B_k[/math] элементом [math]\pi_i[/math], инвариант также будет сохраняться.
- После завершения алгоритма, в очереди [math]B[/math] будут храниться наилучшие элементы для всех возможных длин возрастающих подпоследовательностей последовательности [math]S[/math]. Тогда размер [math]B[/math] равен длине НВП последовательности [math]S[/math].
|
| [math]\triangleleft[/math] |
Пример
Типы операций
- Добавление элемента, который больше всех предыдущих:
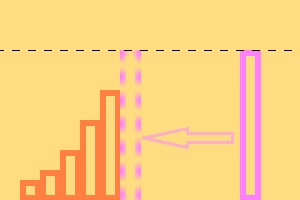
- Замещение элемента более подходящим, т.е. добавление немаксимального элемента:
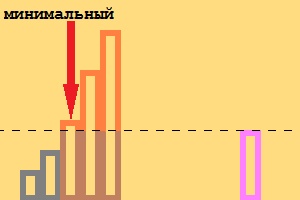[math]\longrightarrow[/math] 
Пример последовательности
| [math]\pi_1[/math] |
[math]\pi_2[/math] |
[math]\pi_3[/math] |
[math]\pi_4[/math] |
[math]\pi_5[/math] |
[math]\pi_6[/math] |
[math]\pi_7[/math] |
[math]\pi_8[/math] |
[math]\pi_9[/math] |
[math]\pi_{10}[/math] |
[math]\pi_{11}[/math] |
[math]\pi_{12}[/math]
|
| [math]9[/math] |
[math]3[/math] |
[math]10[/math] |
[math]4[/math] |
[math]8[/math] |
[math]1[/math] |
[math]2[/math] |
[math]12[/math] |
[math]6[/math] |
[math]5[/math] |
[math]7[/math] |
[math]11[/math]
|
Состояние очереди при каждом добавлении
| [math]B_1[/math] |
[math]B_2[/math] |
[math]B_3[/math] |
[math]B_4[/math] |
[math]B_5[/math] |
[math]~\pi_i~[/math]
|
| 9 |
|
|
|
|
9
|
| 3 |
|
|
|
|
3
|
| [math]3[/math] |
10 |
|
|
|
10
|
| [math]3[/math] |
4 |
|
|
|
4
|
| [math]3[/math] |
[math]4[/math] |
8 |
|
|
8
|
| 1 |
[math]4[/math] |
[math]8[/math] |
|
|
1
|
| [math]1[/math] |
2 |
[math]8[/math] |
|
|
2
|
| [math]1[/math] |
[math]2[/math] |
[math]8[/math] |
12 |
|
12
|
| [math]1[/math] |
[math]2[/math] |
6 |
[math]12[/math] |
|
6
|
| [math]1[/math] |
[math]2[/math] |
5 |
[math]12[/math] |
|
5
|
| [math]1[/math] |
[math]2[/math] |
[math]5[/math] |
7 |
|
7
|
| [math]1[/math] |
[math]2[/math] |
[math]5[/math] |
[math]7[/math] |
11 |
11
|
Псевдокод
int LIS([math]\pi[/math][n])
PriorityQueue B // рабочая приоритетная очередь
int k = 0 // длина НВП
for i = 1 to n
x = [math]\pi[/math][i]
// в любом случае добавляем в очередь очередной элемент
// устаревшие будем удалять
B.insert(x)
if [math]\exists[/math] B.next(x)
// добавленный элемент — не максимальный
// удаляем следующее за x значение
B.delete(B.next(x))
else
// добавленный элемент — максимальный
// предыдущие значения не трогаем, очередь увеличилась
k = k + 1
return k
Расширение алгоритма до нахождения НВП
Основная идея
Будем запоминать пары: для каждого элемента записываем его "предшественника".
Тогда, пройдя по предшественникам, начиная с последнего элемента очереди [math]B[/math], мы можем восстановить НВП.
Общий вид алгоритма
| [math]B_1[/math] |
[math]B_2[/math] |
[math]B_3[/math] |
[math]B_4[/math] |
[math]B_5[/math] |
[math]~\pi_i~[/math]
|
| [math]9[/math] |
|
|
|
|
9
|
| [math]3[/math] |
|
|
|
|
3
|
| [math]3[/math] |
[math]10[/math] |
|
|
|
10
|
| [math]3[/math] |
[math]4[/math] |
|
|
|
4
|
| [math]3[/math] |
[math]4[/math] |
[math]8[/math] |
|
|
8
|
| 1 |
[math]4[/math] |
[math]8[/math] |
|
|
1
|
| 1 |
2 |
[math]8[/math] |
|
|
2
|
| [math]1[/math] |
2 |
[math]8[/math] |
[math]12[/math] |
|
12
|
| [math]1[/math] |
2 |
[math]6[/math] |
[math]12[/math] |
|
6
|
| [math]1[/math] |
2 |
5 |
[math]12[/math] |
|
5
|
| [math]1[/math] |
[math]2[/math] |
5 |
7 |
|
7
|
| [math]1[/math] |
[math]2[/math] |
[math]5[/math] |
7 |
11 |
11
|
| predecessor
|
| [math]1[/math] |
[math]2[/math] |
[math]3[/math] |
[math]4[/math] |
[math]5[/math] |
[math]6[/math] |
[math]7[/math] |
[math]8[/math] |
[math]9[/math] |
[math]10[/math] |
[math]11[/math] |
[math]12[/math]
|
| |
[math]1[/math] |
|
[math]3[/math] |
[math]2[/math] |
[math]2[/math] |
[math]5[/math] |
[math]4[/math] |
|
[math]3[/math] |
[math]7[/math] |
[math]8[/math]
|
Псевдокод
int[] LIS([math]\pi[/math][n])
PriorityQueue B
int k = 0
int predecessor[n] // резервируем [math]n[/math] позиций
for i = 1 to n
x = [math]\pi[/math][i]
B.insert(x)
predecessor[x] = B.prev(x)
if [math]\exists[/math] B.next(x)
B.delete(B.next(x))
else
k = k + 1
// по цепочке от последнего элемента
// восстанавливаем НВП
int result[k]
int cur = B.max
for i = k - 1 downto 0
result[i] = cur
cur = predecessor[cur]
return result
Оптимизация до O(n log log k)
Чтобы Дерево ван Эмде Боаса выполняло операции за [math]O(\operatorname{log}\operatorname{log}k)[/math], необходимо алфавит обрабатываемых значений уменьшить до [math]O(k)[/math].
Предположим, мы знаем такое приближение числа [math]k[/math] числом [math]m: m \geqslant k[/math]. Мы обсудим, как найти такое [math]m[/math] позже.
Чтобы достичь нужной оценки, будем делить последовательность на блоки длины [math]m[/math], кроме последнего, который может быть меньше, и обрабатывать каждый блок отдельно.
Деление на блоки
Последовательность [math]S[/math] делится на блоки [math]C_j,~j=1,~\dots,~\lceil\frac{n}{m}\rceil[/math] элементов:
[math]C_j=(\pi_{(j-1)m+1},\pi_{(j-1)m+2},~\dots~,\pi_{(j-1)m+m)})[/math]
Обозначим за [math]C_j^s[/math] отсортированный блок [math]C_j[/math]. Отсортированные и неотсортированные блоки будем хранить в памяти.
Цифровая сортировка каждых блоков отдельно будет давать нам время рваботы [math]O \left(\dfrac{n}{m}n \right) = O \left(\dfrac{n^2}{m} \right)[/math]. Чтобы отсортировать их за линейное время, дополним каждый элемент номером его блока и получим пары [math]\langle\lceil i/m\rceil,\pi_i\rangle[/math]. Цифровая сортировка этих пар, если принимать за старший разряд номер блока, а за младший значение элемента, будет работать за [math]O(n)[/math], потому что значения элементов и номера блоков не превосходят [math]n[/math].
Обработка блока
Обрабатывая блоки, будем работать не со значениями элементов, а с ключами, которые определенны для каждого элемента внутри блоков. Все блоки будут обрабатываться онлайн, то есть мы не перейдём к обработке следующего блока, пока не закончим с текущим.
Каждому элементу [math]x[/math] взаимно однозначно сопоставим ключ [math]y = \mathtt{key}(x);~x=\mathtt{elt}(y)[/math]. Все значения ключей расположим в промежутке [math]\{1,2,\dots,2m\}[/math], и в очереди [math]B[/math] будем работать со значениями ключей элементов.
Чтобы определить ключи элементов так, чтобы их значения были в представленном промежутке, будем, работая с блоком [math]C_j[/math], сливать элементы, ключи которых находятся в очереди [math]B[/math], с [math]C_j^s[/math] в список [math]\mathtt{merged}[/math].
Получим ключи, сопоставив каждому элементу в [math]\mathtt{merged}[/math] его позицию в этом списке. Как было замечено ранее, элементы, чьи ключи находятся в [math]B[/math], располагаются в возрастающем порядке, поэтому возможно производить тривиальную операцию слияния. Поскольку мы предположили, что [math]m\geqslant k[/math], то количество ключей в [math]B[/math] не больше [math]m[/math], тогда длина [math]\mathtt{merged}[/math] не больше [math]2m[/math], что позволяет однозначно определить ключи на множестве [math]\{1,2,\dots,2m\}[/math].
После того, как мы определили новые ключи для элементов, обновим ключи в очереди [math]B[/math].
Затем запускаем описанный выше алгоритм [math]\mathrm{LIS}[/math], для ключей элементов [math]C_j[/math] в порядке исходной последовательности.
В итоге, обработка блока делится на следующие этапы:
- Достаем из очереди [math]B[/math] ключи [math]x[/math], конвертируем их в элементы [math]\mathtt{elt}(x)[/math] и кладём в список [math]\mathtt{elems}[/math].
- Сливаем элементы в [math]\mathtt{elems}[/math] со следующим отсортированным блоком в список [math]\mathtt{merged}[/math].
- Присваеваем новые ключи элементам в порядке списка [math]\mathtt{merged}[/math].
- Вставляем в [math]B[/math] новые ключи элементов списка [math]\mathtt{elems}[/math].
- Обрабатываем ключи элементов блока в порядке исходной последовательности с помощью алгоритма [math]\mathrm{LIS}[/math]. Для восстановления НВП также используем массив "предшественников", который будет работать с соответствующими ключами элементов [math]\mathtt{elt}(x)[/math].
Доказательство оптимальности
| Утверждение: |
Пусть имеется последовательность [math]S=\{\pi_1,~\dots,~\pi_n\}[/math], разбитая на [math]\lceil n/m \rceil[/math] блоков [math]C_i[/math] длины [math]m[/math]. В результате описанного выше алгоритма получается очередь [math]B[/math], размер которой равен длине НВП последовательности [math]S[/math]. |
| [math]\triangleright[/math] |
|
Докажем, что перед обработкой блока и после его обработки сохраняется инвариант, что очередь [math]B[/math] хранит ключи наилучших элементов для всех возможных длин возрастающих подпоследовательностей обработанной последовательности элементов.
- Пусть перед обработкой блока [math]C_i[/math] соблюдается описанное выражение инварианта для последовательности [math]S_{(i-1)m}=\{\pi_1,~\dots,~\pi_{(i-1)m}\}[/math].
- После слияния элементов очереди [math]B[/math] и блока [math]C_i^s[/math] получаем отсортированный список [math]\mathtt{merged}[/math]. Сопоставив ключи элементам в списке, как их позиции в нём, будет выполняться условие [math](\pi_{u_j}\lt \pi_{u_k} \Longleftrightarrow \mathtt{key}(\pi_{u_j})\lt \mathtt{key}(\pi_{u_k}))[/math], где [math]\pi_{u_j},\pi_{u_k}\in \mathtt{merged}[/math]. Тогда справедливо утверждение, что любая возрастающая последовательность ключей элементов будет соответствовать возрастающей последовательности элементов.
- Во время обработки ключей элементов алгоритм [math]\mathtt{LIS}[/math] работает только с очередью [math]B[/math] и не зависит от предыдущих элементов последовательности, ключи которых не находятся в очереди. Так как на каждой итерации алгоритма [math]\mathrm{LIS}[/math] сохраняется выражение инварианта, что в очереди [math]B[/math] хранятся наилучшие значения ключей элементов, которые соответствуют наилучшим элементам, для всех возможных длин возрастающих подпоследовательностей обработанной подпоследовательности, то в результате работы [math]\mathrm{LIS}[/math] будет очередь [math]B[/math] с ключами, соответствующими наилучшим элементам всех возможных длин возрастающих подпоследовательностей последовательности [math]S_{im}[/math].
- Таким образом, после обработки последнего блока, в очереди [math]B[/math] будут храниться ключи наилучших элементов для каждой длины возрастающих подпоследовательностей последовательности [math]S_n=S[/math]. Тогда последний элемент в очереди [math]B[/math] соответствует наилучшему элементу длины НВП последовательности [math]S[/math], а так как в очереди [math]B[/math] хранятся наилучшие элементы всех возможных длин возрастающих подпоследовательностей [math]S[/math], то размер очереди [math]B[/math] равен длине НВП последовательности [math]S[/math].
|
| [math]\triangleleft[/math] |
Пример
Предположим, что [math]m=5[/math]. Исходно получаем:
| Блок |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
3 |
3
|
| [math]\pi[/math] |
9 |
3 |
10 |
4 |
8 |
1 |
2 |
12 |
6 |
5 |
7 |
11
|
После сортировки:
| Блок |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
3 |
3
|
| [math]\pi[/math] |
3 |
4 |
8 |
9 |
10 |
1 |
2 |
5 |
6 |
12 |
7 |
11
|
Первый блок
| |
| Первый блок
|
| [math]\pi[/math] |
9 |
3 |
10 |
4 |
8
|
| key |
4 |
1 |
5 |
2 |
3
|
|
|
| Cортированный
|
| [math]\pi[/math] |
3 |
4 |
8 |
9 |
10
|
| key |
1 |
2 |
3 |
4 |
5
|
|
Обработка блока с помощью алгоритма [math]\mathrm{LIS}[/math].
| [math]B_1[/math] |
[math]B_2[/math] |
[math]B_3[/math] |
[math]key[/math] |
[math]\pi[/math]
|
| 4 |
|
|
4 |
9
|
| 1 |
|
|
1 |
3
|
| [math]1[/math] |
5 |
|
5 |
10
|
| [math]1[/math] |
2 |
|
2 |
4
|
| [math]1[/math] |
[math]2[/math] |
3 |
3 |
8
|
В результате получаем
[math]B: \{1, 2, 3\}[/math]
[math]\mathtt{merged}: \{3,4,8,9,10\}[/math]
Второй блок
Восстанавливаем элементы [math]B: \{1, 2, 3\}[/math] из [math]\mathtt{merged}: \{3, 4, 8, 9, 10\}[/math]: [math]\{3, 4, 8\}[/math].
Сливаем [math]C_2^s[/math] и восстановленные элементы из [math]B[/math]:
| |
| [math]B[/math]
|
| [math]3[/math] |
[math]4[/math] |
[math]8[/math]
|
|
|
| [math]C_2^s[/math]
|
| [math]1[/math] |
[math]2[/math] |
[math]5[/math] |
[math]6[/math] |
[math]12[/math]
|
|
|
| [math]\mathtt{merged}[/math]
|
| [math]1[/math] |
[math]2[/math] |
[math]3[/math] |
[math]4[/math] |
[math]5[/math] |
[math]6[/math] |
[math]8[/math] |
[math]12[/math]
|
| [math]1[/math] |
[math]2[/math] |
[math]3[/math] |
[math]4[/math] |
[math]5[/math] |
[math]6[/math] |
[math]7[/math] |
[math]8[/math]
|
|
| |
| Второй блок
|
| [math]\pi[/math] |
1 |
2 |
12 |
6 |
5
|
| key |
1 |
2 |
8 |
6 |
5
|
|
|
| Cортированный
|
| [math]\pi[/math] |
1 |
2 |
5 |
6 |
12
|
| key |
1 |
2 |
5 |
6 |
8
|
|
Обновляем ключи в очереди:
| [math]B_1[/math] |
[math]B_2[/math] |
[math]B_3[/math] |
[math]\pi[/math]
|
| 3 |
|
|
3
|
| [math]3[/math] |
4 |
|
4
|
| [math]3[/math] |
[math]4[/math] |
7 |
7
|
запускаем [math]\mathrm{LIS}[/math] для блока:
| [math]B_1[/math] |
[math]B_2[/math] |
[math]B_3[/math] |
[math]B_4[/math] |
[math]key[/math] |
[math]\pi[/math]
|
| 1 |
[math]4[/math] |
[math]7[/math] |
|
1 |
1
|
| [math]1[/math] |
2 |
[math]7[/math] |
|
2 |
2
|
| [math]1[/math] |
[math]2[/math] |
[math]7[/math] |
8 |
8 |
12
|
| [math]1[/math] |
[math]2[/math] |
6 |
[math]8[/math] |
6 |
6
|
| [math]1[/math] |
[math]2[/math] |
5 |
[math]8[/math] |
5 |
5
|
В результате получаем:
[math]B: \{1, 2, 5, 8\}[/math]
[math]\mathtt{merged}: \{1,2,3,4,5,6,8,12\}[/math]
Третий блок
Восстанавливаем элементы [math]B: \{1, 2, 5, 8\}[/math] из [math]\mathtt{merged}: \{1, 2, 3, 4, 5, 6, 8, 12\}[/math]: [math]\{1, 2, 5, 12\}[/math].
Сливаем [math]C_3^s[/math] и восстановленные элементы из [math]B[/math]:
| |
| [math]B[/math]
|
| [math]1[/math] |
[math]2[/math] |
[math]5[/math] |
[math]12[/math]
|
|
|
| [math]C_3^s[/math]
|
| [math]7[/math] |
[math]11[/math]
|
|
|
| [math]\mathtt{merged}[/math]
|
| [math]1[/math] |
[math]2[/math] |
[math]5[/math] |
[math]7[/math] |
[math]11[/math] |
[math]12[/math]
|
| [math]1[/math] |
[math]2[/math] |
[math]3[/math] |
[math]4[/math] |
[math]5[/math] |
[math]6[/math]
|
|
| |
| |
| Третий блок
|
| [math]\pi[/math] |
7 |
11
|
| key |
4 |
5
|
|
|
| Cортированный
|
| [math]\pi[/math] |
7 |
11
|
| key |
4 |
5
|
|
Обновление старых ключей:
| [math]B_1[/math] |
[math]B_2[/math] |
[math]B_3[/math] |
[math]B_4[/math] |
[math]\pi[/math]
|
| 1 |
|
|
|
1
|
| [math]1[/math] |
2 |
|
|
2
|
| [math]1[/math] |
[math]2[/math] |
3 |
|
3
|
| [math]1[/math] |
[math]2[/math] |
[math]3[/math] |
6 |
6
|
запускаем [math]\mathrm{LIS}[/math] для блока:
| [math]B_1[/math] |
[math]B_2[/math] |
[math]B_3[/math] |
[math]B_4[/math] |
[math]B_5[/math] |
[math]key[/math] |
[math]\pi[/math]
|
| [math]1[/math] |
[math]2[/math] |
[math]3[/math] |
4 |
|
4 |
7
|
| [math]1[/math] |
[math]2[/math] |
[math]3[/math] |
[math]4[/math] |
5 |
5 |
11
|
Результат завершения алгоритма:
[math]B: \{1, 2, 3, 4, 5\}[/math]
[math]\mathtt{merged}: \{1,2,5,7,11,12\}[/math]
Получаем, что длина НВП — [math]5[/math], и НВП оканчивается на [math]\mathtt{merged}[5]=11[/math].
Восстановление НВП
| [math]\mathtt{predecessor}[/math]
|
| [math]1[/math] |
[math]2[/math] |
[math]3[/math] |
[math]4[/math] |
[math]5[/math] |
[math]6[/math] |
[math]7[/math] |
[math]8[/math] |
[math]9[/math] |
[math]10[/math] |
[math]11[/math] |
[math]12[/math]
|
| |
[math]1[/math] |
|
[math]3[/math] |
[math]2[/math] |
[math]2[/math] |
[math]5[/math] |
[math]4[/math] |
|
[math]3[/math] |
[math]7[/math] |
[math]8[/math]
|
Начинаем восстановление с [math]\mathtt{merged}[5] = 11[/math]:
| обратный порядок |
[math]11[/math] |
[math]7[/math] |
[math]5[/math] |
[math]2[/math] |
[math]1[/math]
|
| НВП |
[math]1[/math] |
[math]2[/math] |
[math]5[/math] |
[math]7[/math] |
[math]11[/math]
|
Оценка времени работы
Так как размер списка [math]\mathtt{merged}[/math] не больше [math]2m[/math], а количество блоков всего [math]\lceil n/m \rceil[/math]. То общее количество присваиваний новых ключей элементам последовательности, также как и количество операций слияния списков, не больше [math]2cm\cdot\dfrac{n}{m}=O(n)[/math], где c — некоторая константа. Каждая операция с приоритетной очередью требует [math]O(\log \log m)[/math] времени, так как элементы в [math]B[/math] не больше [math]2m[/math].
Рассмотрим последовательность [math]\{m_0,~m_1,~m_2,~\dots\}[/math], где [math] m_{i+1} = m_i ^{\operatorname{log}m_i} = 2^{\operatorname{log}^2m_i}[/math], [math]m_0[/math] — некоторое значение, меньшее [math]k[/math].
Будем по порядку для элементов этой последовательности запускать алгоритм, представленный выше. Если размер очереди [math]B[/math] становится больше [math]m_i[/math], то условие [math]m \geqslant k[/math] перестает выполняться, тогда останавливаем алгоритм и переходим к следующему значению [math]m_{i+1}[/math]. Когда найдётся первое [math]m_j:m_j\geqslant k[/math], то алгоритм успешно завершится.
Таким образом, время работы запущенного алгоритма — [math]O(n \log \log {m_i})[/math] для [math]0\leqslant i \leqslant j[/math].
Заметим, что
[math]\operatorname{log}\operatorname{log}m_{i+1} = \operatorname{log}\operatorname{log}2^{\operatorname{log}^2m_i} = \operatorname{log}\operatorname{log}^2m_i = 2\operatorname{log}\operatorname{log}m_i[/math].
[math]\operatorname{log}\operatorname{log}m_j = 2^{j-i}\operatorname{log}\operatorname{log}m_i[/math]
Общее время работы алгоритма по всем [math]m_i[/math] — [math]O(n(\sum_{i=0}\limits^{j}{2^{-(i-1)}})\log \log m_i)[/math].
Обратим внимание, что [math]m_i \lt k^{\operatorname{log}k}[/math], так как в противном случае [math]m_{i-1} \gt k[/math], что противоречит тому, что [math]m_i[/math] — первый из тех, которые больше [math]k[/math]. Следовательно, [math]\operatorname{log}\operatorname{log}m_i \lt 2\operatorname{log}\operatorname{log}k \[/math].
Тогда алгоритм также работает за время [math]O(n\operatorname{log}\operatorname{log}k)[/math].
См. также
Источники информации
|
