| Определение: |
Определим [math]P=(Q,\Sigma,\Gamma,\delta,q_0,Z_0,F)[/math] как детерминированный автомат с магазинной (стековой) памятью, где
- [math]Q[/math]: конечное множество состояний.
- [math]\Sigma[/math]: конечное множество входных символов.
- [math]\Gamma[/math]: конечный магазинный алфавит — множество символов, которые можно помещать в магазин.
- [math]\delta[/math]: функция переходов. [math]\delta (q,a,X)=(p,\gamma)[/math], где для кадой тройки [math](q,a,X)[/math] пара [math](p,\gamma)[/math] задана единственным образом, где
- [math]q[/math]: текущее состояние из Q.
- [math]a[/math]: входной символ.
- [math]X[/math]: магазинный символ из [math]\Gamma[/math].
- [math]p[/math]: новое состояние из Q.
- [math]\gamma[/math]: цепочка магазинных символов, замещающих [math]X[/math] на вершине магазина.
- [math]q_0[/math]: начальное состояние.
- [math]Z_0[/math]: начальный магазинный символ (маркер дна). Находится в магазине в начале работы автомата.
- [math]F[/math]: множество допускающих состояний.
|
Будем обозначать переход автомата из состояния [math](q_1,a_1,X_1)[/math] в состояние [math](q_2,a_2,X_2)[/math] как [math](q_1,a_1,X_1)\vdash(q_2,a_2,X_2)[/math]. Переход автомата из состояния [math](q_1,a_1,X_1)[/math] в состояние [math](q_{p+1},a_{p+1},X_{p+1})[/math] через [math]P[/math] промежуточных состояний обозначаем [math](q_1,a_1,X_1)\vdash^*_P(q_{p+1},a_{p+1},X_{p+1})[/math].
Пример
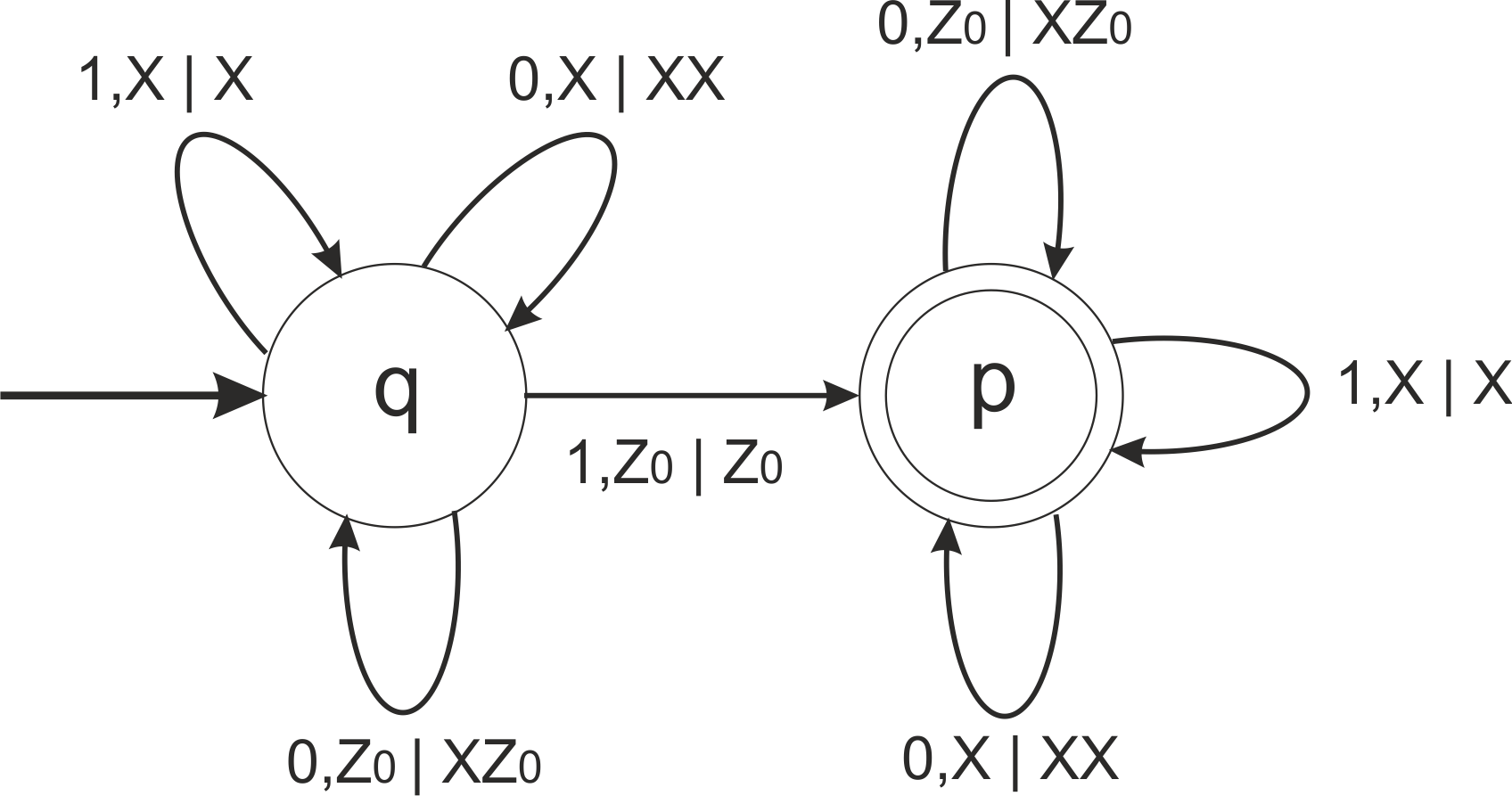
Автомат [math]P=(\{q,p\},\{0,1\},\{Z_0,X\},\delta,q,Z_0,\{p\})[/math] с функией перехода [math]\delta[/math]:
- [math]\delta(q,0,Z_0)=(q,XZ_0)[/math]
- [math]\delta(q,0,X)=(q,XX)[/math]
- [math]\delta(q,1,X)=(q,X)[/math]
- [math]\delta(q,0,Z_0)=(p,Z_0)[/math]
- [math]\delta(p,0,Z_0)=(p,XZ_0)[/math]
- [math]\delta(p,0,X)=(p,XX)[/math]
- [math]\delta(p,1,X)=(p,X)[/math]