Batch-normalization

Нормализация батчей (англ. batch-normalization) — это метод, который позволяет повысить производительность и стабилизировать работу искусственных нейронных сетей. Суть данного метода заключается в том, что некоторым слоям нейронной сети на вход подаются данные, предварительно обработанные и имеющие нулевое среднее значение и единичную дисперсию. Впервые данный метод был представлен в .

Идея

Нормализация входного слоя обычно выполняется путем масштабирования функции активации. Например, когда у нас есть признаки со значениями от 0 до 1 и некоторые признаки со значениями от 1 до 1000, то их необходимо нормализовать, чтобы ускорить обучение. То же самое можно сделать и для скрытых слоев нейронных сетей.

Нормализация батчей уменьшает величину, на которую смещаются значения узлов в скрытых слоях (т.н. смещение ковариации (англ. covariance shift)). Проиллюстрируем смещение ковариации примером. Пусть есть глубокая нейронная сеть, которая обучена обнаруживать кошек на изображении. И нейронная сеть была обучена на изображении только черных кошек. Теперь, если попытаться использовать обученную модель для обнаружения цветных кошек, то, очевидно, результат будет неудовлетворительный. Обучающая и тестовая выборки содержат изображения кошек, но немного отличаются. Другими словами, если модель обучена отображению из множества [math]X[/math] в множество [math]Y[/math] и если распределение элементов в [math]X[/math] изменяется, то появляется необходимость обучить модель заново, чтобы "выровнять" распределение элементов в [math]X[/math] и [math]Y[/math].

Кроме того, нормализация батчей имеет несколько приемуществ:

• более быстрая сходимость моделей, несмотря на добавление новых вычислений;
• позволяет каждому слою сети обучатся более независимо от других слоев;
• становится возможно использование более высокого коэффициента скорости обучения, так как нормализация батчей гарантирует, что выходы узлов нейронной сети не будут иметь слишком больших или малых значений;
• нормализация батчей в каком-то смысле также является механизмом регуляризации: данный метод привносит в выходы узлов скрытых слоев некоторый шум, аналогично методу dropout;
• модели становятся менее чувствительны к начальной инициализации весов.

Описание метода

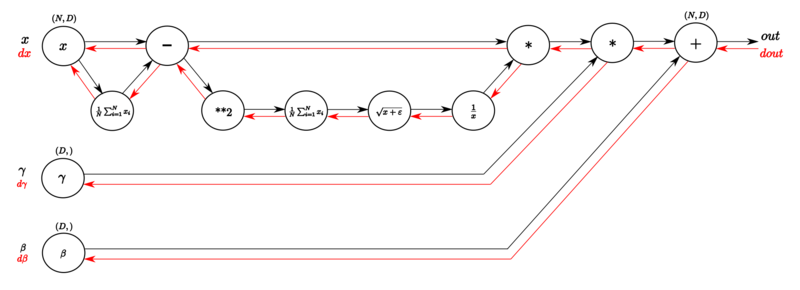
Опишем устройство метода нормализации батчей. Пусть, на вход некоторому слою нейронной сети поступает вектор размерности [math]d[/math]: [math]x = (x^{(1)}, \ldots, x^{(d)})[/math]. Нормализуем данный вектор по каждой размерности [math]k[/math]:

[math]\hat{x}^{(k)} = \displaystyle \frac{x^{(k)} - E(x^{(k)})}{\sqrt{D(x^{(k)})}}[/math],

где математическое ожидание и дисперсия считаются по всей обучающей выборке. Такая нормализация входа слоя нейронной сети может изменить представление данных в слое. Чтобы избежать данной проблемы, вводятся два параметра сжатия и сдвига нормализованной величины для каждого [math]x_{k}[/math]: [math]\gamma_{k}[/math], [math]\beta_{k}[/math] — которые действуют следующим образом:

[math]y^{(k)} = \gamma^{(k)} \hat{x}^{(k)} + \beta^{(k)}[/math].

Данные параметры настраиваются в процессе обучения вместе с остальными гиперпараметрами модели.

Пусть, обучение модели производится с помощью батчей [math]B[/math] размера [math]m[/math]: [math]B = \{x_{1,\ldots, m}\}[/math]. Здесь нормализация применяется к каждой компоненте входа с номером [math]k[/math] отдельно, поэтому в [math]x^{(k)}[/math] индекс опускается для ясности изложения. Пусть, были получены нормализованные значения батча [math]\hat{x}_{1,\ldots, m}[/math]. Далее, после применения операций сжатия и сдвига были получены [math]y_{1,\ldots, m}[/math]. Обозначим данную функцию нормализации батчей следующим образом:

[math]BN_{\gamma, \beta}: x_{1,\ldots, m} \rightarrow y_{1,\ldots, m}[/math]

Тогда, алгоритм нормализации батчей можно представить так:

Вход: значения [math]x[/math] из батча [math]B = \{x_{1,\ldots, m}\}[/math]; настраиваемые параметры [math]\gamma, \beta[/math]; константа [math]\epsilon[/math] для вычислительной устойчивости.
Выход: [math]\{y_{i} = BN_{\gamma, \beta}(x_{i})\}[/math]
[math]\mu_{B} = \displaystyle \frac{1}{m} \sum_{i=1}^{m} x_{i}[/math] // математическое ожидание батча
[math]\sigma_{B}^{2} = \displaystyle \frac{1}{m} \sum_{i=1}^{m} (x_{i} - \mu_{B})^{2}[/math] // дисперсия батча
[math]\hat{x}_{i} = \displaystyle \frac{x_{i} - \mu_{B}}{\sqrt{\sigma_{B}^{2} + \epsilon}}[/math] // нормализация
[math]y_{i} = \gamma \hat{x}_{i} + \beta \equiv BN_{\gamma, \beta}(x_{i}) [/math] // сжатие и сдвиг

Обучение нейронных сетей с нормализацией батчей

Схема обработки слоя нормализации батчей алгоритмом обратного распространения ошибки. Слева-направо черными стрелками показана работа алгоритма в прямом направлении. А справа-налево красными стрелками — в обратном направлении, где вычисляется градиент функции потерь. Здесь [math]N=m[/math] и [math]D=d[/math]

Для обучения нейронных сетей необходимо вычислять градиент функции потерь [math]l[/math]. В случае использования метода нормализации батчей градиент вычисляется следующим образом:

[math]\displaystyle \frac{\partial l}{\partial \hat{x}_{i}} = \frac{\partial l}{\partial y_{i}} \cdot \gamma[/math]

[math]\displaystyle \frac{\partial l}{\partial \sigma_{B}^{2}} = \sum_{i=1}^{m}\frac{\partial l}{\partial \hat{x}_{i}} \cdot (x_{i} - \mu_{B}) \cdot \frac{-1}{2}(\sigma_{B}^{2} + \epsilon)^{-3/2}[/math]

[math]\displaystyle \frac{\partial l}{\partial \mu_{B}} = \left(\sum_{i=1}^{m}\frac{\partial l}{\partial \hat{x}_{i}} \cdot \frac{-1}{\sqrt{\sigma_{B}^{2} + \epsilon}}\right) + \frac{\partial l}{\partial \sigma_{B}^{2}} \cdot \frac{\sum_{i=1}^{m}-2(x_{i}-\mu_{B})}{m}[/math]

[math]\displaystyle \frac{\partial l}{\partial x_{i}} = \frac{\partial l}{\partial \hat{x}_{i}} \cdot \frac{1}{\sqrt{\sigma_{B}^{2} + \epsilon}} + \frac{\partial l}{\partial \sigma_{B}^{2}} \cdot \frac{2(x_{i}-\mu_{B})}{m} + \frac{\partial l}{\partial \mu_{B}} \cdot \frac{1}{m}[/math]

[math]\displaystyle \frac{\partial l}{\partial \gamma} = \sum_{i=1}^{m}\frac{\partial l}{\partial y_{i}} \cdot \hat{x}_{i}[/math]

[math]\displaystyle \frac{\partial l}{\partial \beta} = \sum_{i=1}^{m}\frac{\partial l}{\partial y_{i}}[/math]

Нормализация батчей в свёрточных сетях

Нормализация батчей может быть применена к любой функции активации. Рассмотрим подробнее случай аффинного преобразования с некоторой нелинейной функцией:

[math]z = g(Wu + b)[/math],

где [math]W[/math] и [math]b[/math] настраиваемые параметры модели, а [math]g(\cdot)[/math] некоторая нелинейная функция, например cигмоида или ReLU. Данной функцией можно описать как обычные, так и сверточные слои нейронных сетей. Так, нормализация батчей применяется сразу перед нелинейной функцией [math]g(\cdot)[/math] к [math]x = Wu + b[/math]. Параметр [math]b[/math] может быть проигнорирован последующим вычитание математического ожидания (затем роль этого параметра будет играть [math]\beta[/math]). Поэтому [math]z = g(Wu + b)[/math] может быть записано так:

[math]z = g(BN(Wu))[/math],

где [math]BN[/math] применяется отдельно к каждой размерности [math]x=Wu[/math] с отдельной парой параметров [math]\gamma^{(k)}[/math] и [math]\beta^{(k)}[/math] для каждой размерности.

В случае свёрточных сетей, дополнительно необходима нормализация, чтобы удовлетворить свойство свёрточных сетей, что различные элементы в разных местах одной карты признаков должны быть нормализованны одинаково. Чтобы этого добиться, нормализация выполняется совместно над всеми значениями в батче. Пусть, [math]B[/math] — множество всех значений в карте признаков по всему батчу и всем точкам в карте признаков. Тогда для батча размера [math]m[/math] и карты признаков размера [math]p \times q[/math] размер [math]B[/math] равен [math]m'=|B|=m \cdot pq[/math]. Тогда, параметры [math]\gamma^{(k)}[/math] и [math]\beta^{(k)}[/math] настраиваются для каждой карты признаков отдельно.

Источники информации

• Glossary of Deep Learning: Batch Normalisation
• Understanding the backward pass through Batch Normalization Layer