Дерево решений и случайный лес

Дерево решений

Определение:

Дерево решений (англ. decision tree, DT) — алгоритм классификации [math]a(x)[/math], задающийся деревом (связным ациклическим графом): Множество вершин [math] V = V_{внутр} \cup V_{лист} [/math], [math]v_0 \in V[/math] — корень дерева Для [math]v \in V_{внутр}[/math] определены функции: [math] f_v : X \rightarrow D_v [/math] и [math] D_v : X \rightarrow V [/math], [math]D_v \lt \infty[/math] Для [math]v \in V_{лист}[/math] определена метка класса [math]y_v \in Y[/math]

Классификация объекта [math] x \in X [/math] бинарным решающим деревом

Y classify(x):
  [math]v = v_0[/math]
  while [math]v \in V_{внутр}[/math]:
    [math]v := S_v[/math]([math]f_v[/math](x)) ;
  return [math]y_v[/math]

Определение:

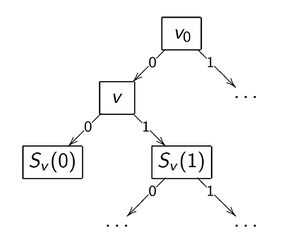
Бинарное решающее дерево — это алгоритм классификации, задающийся бинарным деревом, в котором каждой внутренней вершине [math] v \in V [/math] приписан предикат [math] \beta_v : X \rightarrow {0, 1} [/math], каждой терминальной вершине [math] v \in V [/math] приписано имя класса [math] c_v \in Y [/math]. При классификации объекта [math] x \in X [/math] он проходит по дереву путь от корня до некоторого листа, в соответствии с Алгоритмом 1.5.

Разновидности решающих деревьев

Тип задачи

• Классификация
• Регрессия

Критерии ветвления

• Энтропийный критерий
• Критерий Джини

Передача информации между вершинами

• (alternating decision tree)

Рецукция решающих деревьев

• Предредукция
• Постредукция

Алгоритмы построения решающих деревьев

• Алгоритм ID3
• Алгоритм C4.5
• Алгоритм C5.0
• Алгоритм CART
• Алгоритм LISTBB

Композиции решающих деревьев

• Решающий лес
• Бустинг над решающими деревьями

Ссылки

• Classification and Regression Trees — лекции Cosma Shalizi, ноябрь 2009.