CAP теорема
CAP-теорема — утверждение о том, что в распределённых системах нельзя одновременно добиться трёх свойств:
- Consistency — на всех не отказавших узлах одинаковые (с точки зрения пользователя) данные
- Availability — запросы ко всем не отказавшим узлам возвращают ответ
- Partition tolerance — даже если связь в системе стала нестабильной (вплоть до разделения системы на куски), то система продолжает работать
Формально мы это не формулировали и не доказывали. Оригинальная формулировка — Brewer's Conjecture (2000), а формализовано в работе Gilbert & Lynch (2004). Там есть много тонкостей с тем, что такое "не отказавший узел", "одинаковые данные", "разрыв связи", "система продолжает работать", "когда система всё-таки окончательно ломается и считается недоступной" и тому подобное.
Для общей эрудиции выглядят неплохо статьи[1][2]
Классификация алгоритмов
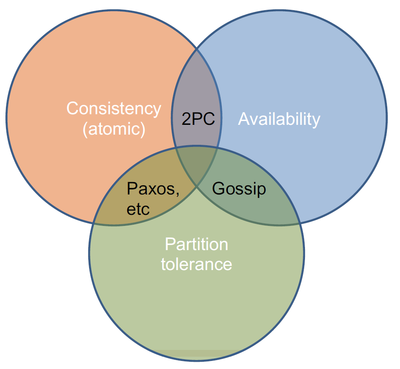
А вот алгоритмы, которые удовлетворяют хотя бы двум свойствам, можно нарисовать на диаграмма Венна:
Дальше идут объяснения с лекции, они отличаются в разных источниках (например, много где 2PC идёт вместе с Paxos в CP, а не в CA), а где-то совпадают с лекцией[3].
- Если мы хотим согласованность и доступность, то используем протокол двухфазного коммита: он гарантирует нам согласованное состояние глобально во всей системе и мы всегда можем обслуживать запросы. Но если потерялась связь, то какие-то запросы нельзя обработать, потому что часть данных может быть на одном узле, а часть на другом. Каждый кусок всё ещё будет работать по отдельности, но глобальные транзакции выполнять мы не сможем.
- Иногда нам не так важна согласованность и мы согласны на простую eventual consistency — это когда информация может быть доступна не сразу везде, а только через какое-то время, если система здорова. Сюда идут gossip-протоколы.
- Если мы хотим согласованность и толерантность к разделению, то надо жертвовать доступностью. Например, при помощи Paxos мы можем хранить все данные сразу на всех узлах, но тогда узлы, оказавшиеся в меньшинстве, ничего сделать не могут.