Подсчет деревьев

Материал из Викиконспекты
Перейти к: навигация, поиск
НЕТ ВОЙНЕ

24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян.

Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием.

Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей.

Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить.

Антивоенный комитет России

Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.
meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки.

Описание всех используемых далее комбинаторных объектов можно найти в статье "конструирование комбинаторных объектов и их подсчёт".

Непомеченные деревья

Бинарные деревья

Утверждение:
Число непомеченных бинарных деревьев [math]T_n[/math] равно [math]C_{n}[/math] ([math]n[/math]-ое число Каталана).
[math]\triangleright[/math]

Устройство бинарного дерева в терминах комбинаторных классов выражается следующим образом [math]T = \varepsilon + z\times T\times T[/math].
В терминах производящих функций эта конструкция выглядит следующим образом [math]T(s) = 1 + s{T(s)}^2[/math]. Решением данного уравнения будет [math]T(s) = \frac{1 - \sqrt{1 - 4s}}{2s}[/math]. Тогда:

[math]T_{n} = Pair(T, \; T_{n-1}) = \sum\limits_{i=0}^{n-1}T_{i}T_{n-i-1}=C_{n}[/math], где [math]C_{n}[/math] — [math]n[/math]-ое число Каталана.
[math]\triangleleft[/math]
Утверждение:
Производящая функция числа непомеченных полных бинарных деревьев: [math]T(s) = \frac{1 - \sqrt{1 - 4s^2}}{2s}[/math].
[math]\triangleright[/math]

Устройство бинарного дерева в терминах комбинаторных классов выражается следующим образом [math]T = z + z\times T\times T[/math].
В терминах производящих функций эта конструкция выглядит следующим образом [math]T(s) = s + s{T(s)}^2[/math].

Решением данного уравнения будет [math]T(s) = \frac{1 - \sqrt{1 - 4s^2}}{2s}[/math].
[math]\triangleleft[/math]

Подвешенные непомеченные деревьея с порядком на детях

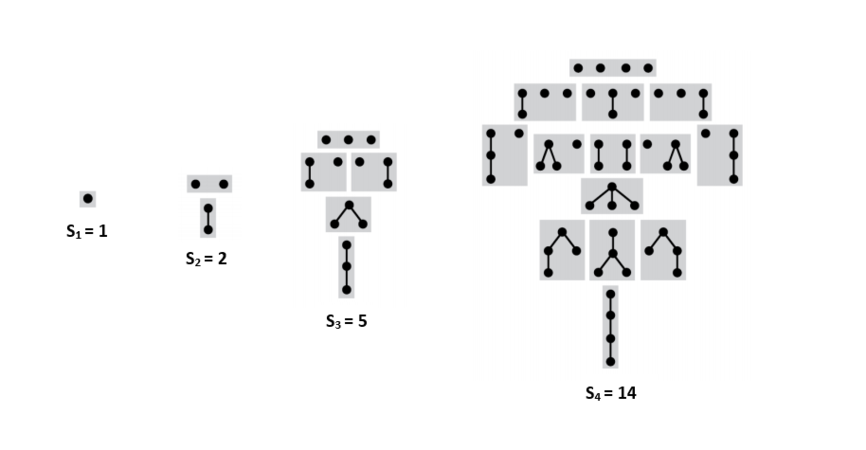
Пусть [math]T_{n}[/math] — количество таких деревьев с [math]n[/math] вершинами. [math]S=Seq(A)[/math] — множество всех последовательностей из данных деревьев. [math]S_{n}[/math] — количество последовательностей с суммарным количество вершин [math]n[/math]. Чтобы получить дерево из [math]n[/math] вершин, достаточно взять [math]1[/math] вершину, и подвесить к ней последовательность деревьев с суммарным количеством вершин [math]n-1[/math]. Тогда:

[math]T_{n}=S_{n-1}[/math].
[math]S_{n}=\sum\limits_{i=1}^{n} T_{i} S_{n-i}=\sum\limits_{i=1}^{n} S_{i-1} S_{n-i}=\sum\limits_{i=0}^{n-1} S_{i} S_{n-i-1}=C_{n}[/math], где [math]C_{n}[/math] — [math]n[/math]-ое число Каталана.

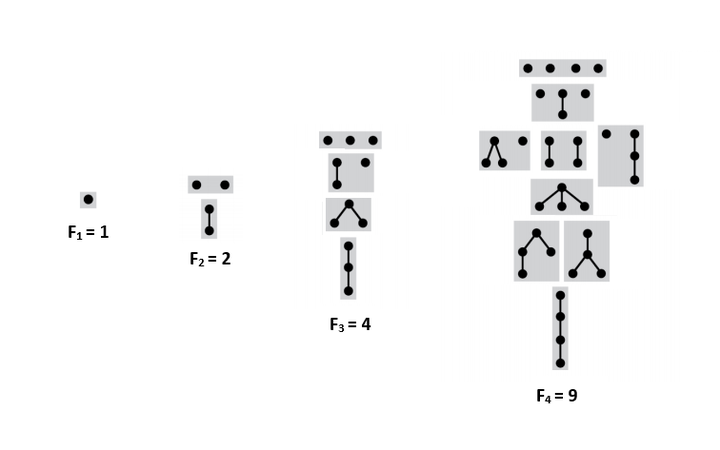
  • Последовательность корневых деревьев

  • Последовательность помеченных корневых деревьев

Подвешенные непомеченные деревья без порядка на детях

Пусть [math]T_{n}[/math] — количество таких деревьев с [math]n[/math] вершинами. [math]F=MSet(T)[/math] — множество всех лесов из данных деревьев, так как лес можно интерпретировать как мультимножество из деревьев. [math]F_{n}=f_{n,n}[/math] — количество лесов с суммарным количество вершин [math]n[/math]. [math]f_{n, k}[/math] — количество таких лесов из [math]n[/math] вершин, что деревья в них содержат не более чем [math]k[/math] вершин. Чтобы получить дерево из [math]n[/math] вершин, достаточно взять [math]1[/math] вершину и подвесить к ней лес деревьев с суммарным количеством вершин [math]n-1[/math]. Тогда:

[math]T_{n}=F_{n-1}[/math].
[math]F_{n}=f_{n, n}[/math].
[math]f_{n,k}=\sum\limits_{i=0}^{\lfloor \frac{n}{k} \rfloor} \binom{T_{k + i - 1}}{i} s_{n-ik, k-1}[/math].

Количество таких деревьев с [math]n[/math] вершинами образуют последовательность A000081[1].

  • Последовательность леса

  • Последовательность корневых деревьев

Помеченные деревья

Определение:
Помеченное дерево c [math]n[/math] вершинами - дерево c [math]n[/math] вершинами, вершинам которого взаимно однозначно соответствуют числа от 1 до n.


Теорема (Кэли):
Число помеченных деревьев с [math]n[/math] вершинами равно [math]n^{n - 2}[/math].
Доказательство:
[math]\triangleright[/math]

Можно доказать формулу двумя способами.

Первый способ.

Так как между помеченными деревьями c [math]n[/math] вершинами и последовательностями длины [math]n - 2[/math] из чисел от [math]1[/math] до [math]n[/math] существует биекция (Код Прюфера), то количество помеченных деревьев совпадает с количеством последовательностей длины [math]n - 2[/math] из чисел от [math]1[/math] до [math]n = n^{n - 2}[/math].

Второй способ.

С помощью матрицы Кирхгофа для полного графа на [math]n[/math] вершинах. Число помеченных деревьев c [math]n[/math] вершинами, очевидно, равно числу остовов в полном графе [math]K_n[/math], которое есть [math]n^{n-2}[/math] по следствию теоремы Кирхгофа.
[math]\triangleleft[/math]
Утверждение:
Число помеченных корневых деревьев с [math]n[/math] вершинами есть [math]T_n = n^{n - 1}[/math].
[math]\triangleright[/math]

Данное утверждение является следствием теоремы Кэли.
Обозначим через [math]T_n[/math] число корневых помеченных деревьев с [math]n[/math] вершинами, т.е. число помеченных деревьев, в которых одна из вершин выделена и названа корнем.

Число корневых помеченных деревьев с [math]n[/math] вершинами в [math]n[/math] раз больше числа помеченных деревьев с [math]n[/math] вершинами: в качестве корня можно выбрать любую из [math]n[/math] различных вершин.
[math]\triangleleft[/math]

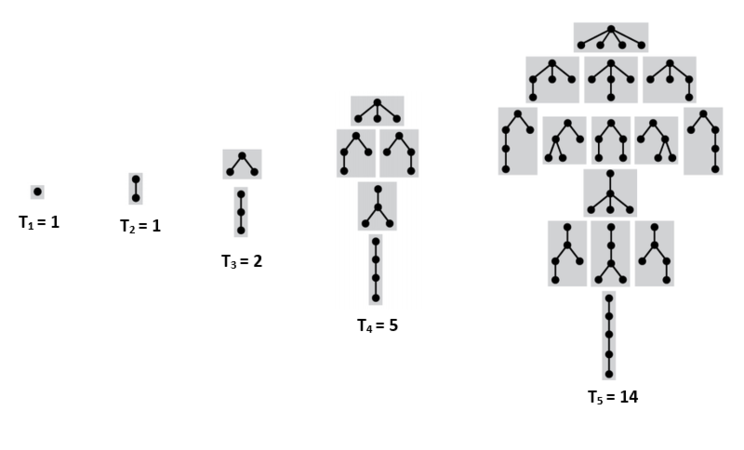
Подвешенные помеченные деревья с порядком на детях

Утверждение:
Число помеченных корневых деревьев с [math]n[/math] вершинами с порядком на детях есть [math]T_n = n!\cdot C_n[/math].
[math]\triangleright[/math]

Как и в непомеченном случае, структура объекта остается неизменной:

[math]T = U\times Seq(T)[/math]

Производящая функция будет иметь вид:

[math]T(s) = s\dfrac{1}{1 - T(s)} \iff T(s) = \sum\limits_{n=1}^{\infty} \dfrac{1 - \sqrt{1 - 4s}}{2} \iff T(s) = \sum\limits_{n=1}^{\infty} \dfrac{C_nn!}{n!}s^n[/math]
Таким образом, число помеченных корневых деревьев с [math]n[/math] с порядком на детях вершинами есть [math]T_n = n!\cdot C_n[/math]
[math]\triangleleft[/math]

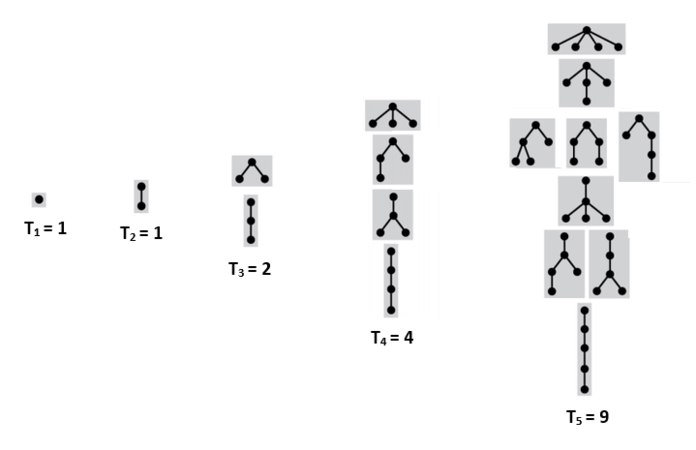
Подвешенные помеченные деревья без порядка на детях

Утверждение:
Как и в непомеченном случае, структура объекта остается неизменной: [math]T = U\times Set(T)[/math].
Производящая функция будет иметь вид: [math]T(s) = s\cdot e^{T(s)}[/math]

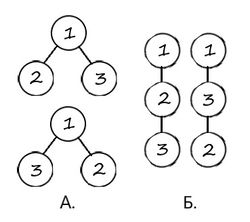
В предыдущем пункте порядок на детях однозначно задавал, как будут располагаться поддеревья, теперь же подсчёт оказывается сложнее:

Marked trees no order example.jpg



В данном примере в А два представленных дерева — одинаковые, а в B — разные.
Для [math]T(s)[/math] нет однозначно выражаемой формулы. Однако, [math]T_n[/math] можно получить, раскрыв экспоненту до [math]n[/math]-ого члена, а именно [math]e^{T(s)} = \sum\limits_{k = 0}^{n}\dfrac{(T(s))^k}{k!}[/math]
Более подробное объяснение происходящего можно посмотреть в лекции[2].




См.также

Литература

  1. ↑ Number of unlabeled rooted trees with n node
  2. ↑ Станкевич А.С. Лекции по дискретной математике // Помеченные объекты и экспоненциальные ПФ, 2020. URL: https://youtu.be/6qQQj6G8-tA?t=4391
Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Подсчет_деревьев&oldid=82855»