Этапы обработки запроса. Перезапись запросов
В этом разделе будут рассмотрен этап обработки запросов, а именно перезапись запросов
Содержание
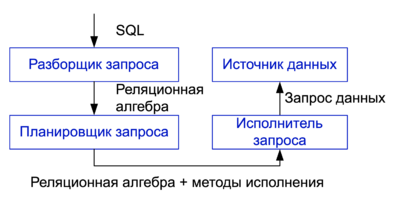
Обработка запроса
Мотивирующий пример
Пусть есть следующая база данных:
- Students(SId, FirstName, LastName, GId, Year)
- $10^4$ записей
- Индексы: (SId) (кластеризованный), (GId)
- Groups(GId, Name)
- $10^3$ записей
- Индексы: (GId) (кластеризованный), (Name)
И следующий запрос:
Фамилии студентов группы M3439
select LastName from Students natural join Groups where Name = 'M34391'
Планы запросов без индексов
- План 1
- $π_{FirstName}(σ_{Name=M34391}(σ_{S.GId=G.GId}(S × G)))$
- $10^4·10^3 + 10^4·10^3 + 10^4 + 20 ≈ 2·10^7$ операций
- План 2
- $π_{Name}(σ_{Name=M34391}(S ⋈ G))$
- $10^4·10^3 + 10^4 + 20 ≈ 10^7$ операция
- План 3
- $π_{Name}(S ⋈ σ_{Name=M34391}(G))$
- $10^3 + 10^4 + 20 ≈ 10^4$ операций
Планы запросов с индексами
- План 4. Students(GId)
- $π_{Name}(S ⋈ σ_{Name=M34391}(G))$
- $10^3 + (3 + 20) + 20 ≈ 10^3$ операций
- План 5. Groups(Name), Students(GId)
- $π_{Name}(S ⋈ σ_{Name=M34391}(G))$
- $2 + (3 + 20) + 20 ≈ 45$ операций
От выбора плана сильно зависит производительность
Наиболее медленный план $2·10^7$ операций
Наиболее быстрый план $45$ операций
Обработка запроса
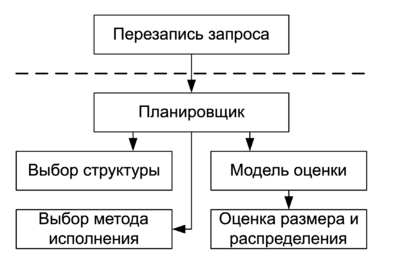
Перезапись и планировщик
- Перезапись запроса
- Статические правила оптимизации запроса
- Считается, что полезны всегда
- Планировщик запроса
- Оптимизация в зависимости от данных
- Перебор вариантов
Выбор структуры и метода
- Выбор структуры
- Преобразование запроса
- Порядок выполнения операций
- Порядок соединений
- Выбор метода исполнения
- Как исполняется каждая операция
Оценка плана
- Модель стоимости
- Стоимость операции
- Размер операндов
- Размер результата
- Оценка размера и распределения
- Статистика по данным
- Статистика предыдущих запросов
Перезапись запроса
Минимизация набора операций
Преобразование подзапросов
- Преобразуются в реляционную алгебру
- Запись в реляционном исчислении
- Вынос кванторов
- Преобразование в алгебру
Преобразование соединений
- Внешние соединения
- $R_1 \ojoin_θ R_2 ⇒ (R_1 \ljoin_θ R_2) ∪ (R_1 \rjoin_θ R_2)$
- $R_1 \ljoin_θ R_2 ⇒ σ_θ(R_1 × R_2) ∪ (R_1 - π_{R_1}(σ_θ(R_1 × R_2)))$
- $R_1 \rjoin_θ R_2 ⇒ σ_θ(R_1 × R_2) ∪ (R_2 - π_{R_2}(σ_θ(R_1 × R_2)))$
- Декартово соединение
- $R_1 × R_2 ⇒ R_1 ⋈ R_2$
Унарные операции
Повторная фильтрация
- Правило
- Повторное применение фильтрации заменяется одинарным
- $σ_{cond_1}(σ_{cond_2}(R)) ⇒ σ_{cond_1 ∧ cond_2}(R)$
- Пример
- $π_{FirstName}(σ_{Name=M34391}(σ_{S.GId=G.GId}(S × G))) ⇒ π_{FirstName}(σ_{Name=M34391 ∧ S.GId=G.GId}(S × G))$
Повторная проекция
- Правило
- Повторное применение проекции заменяется внешней
- $π_{A}(π_{B}(R)) ⇒ π_{A}(R)$
- Пример
- $π_{FirstName}(π_{FirstName, Name}(S × G)) ⇒ π_{FirstName}(S × G)$
Проекция и фильтрация
- Правило
- Фильтрация осуществляется до проекции
- $σ_{cond}(π_{A}(R)) ⇒ π_{A}(σ_{cond}(R))$
- Пример
- $π_{FirstName}(σ_{Name=M34391}(π_{FirstName, Name}(S × G))) ⇒ $
- $π_{FirstName}(π_{FirstName, Name}(σ_{Name=M34391}(S × G))) ⇒ $
- $π_{FirstName}(σ_{Name=M34391}(S × G))$
Алгебраические свойства операций
Дистрибутивность операций
- Фильтрация
- $σ_{cond}(R_1 ∪ R_2) ⇒ σ_{cond}(R_1) ∪ σ_{cond}(R_2)$
- $σ_{cond}(R_1 \cap R_2) ⇒ σ_{cond}(R_1) \cap σ_{cond}(R_2)$
- $σ_{cond}(R_1 - R_2) ⇒ σ_{cond}(R_1) - σ_{cond}(R_2)$
- $σ_{cond_1 ∧ cond_2}(R_1 ⋈ R_2) ⇒ σ_{cond_1}(R_1) ⋈ σ_{cond_2}(R_2)$
- Проекция
- $π_A(R_1 ∪ R_2) ⇒ π_A(R_1) ∪ π_A(R_2)$
- $π_A(R_1 ∩ R_2) ⇏ π_A(R_1) ∩ π_A(R_2)$
- $π_A(R_1 - R_2) ⇏ π_A(R_1) - π_A(R_2)$
- $π_{A}(R_1 ⋈ R_2) ⇒ π_A(π_{(A ∪ R_2) ∩ R_1}(R_1) ⋈ π_{(A ∪ R_1) ∩ R_2}(R_2))$
Коммутативность операций
Коммутативные операции
$⋈$, $∪$, $∩$
Некоммутативные операции
$-$
$\div$, $\gdiv$
Применение коммутативности
Выбор левой и правой стороны для несимметричных методов исполнения
Ассоциативность операций
Ассоциативные операции
$⋈$, $∪$, $∩$
Неассоциативные операции
$-$
$\div$, $\gdiv$
Применение ассоциативности
Выбор порядка выполнения операций
Обработка условий
Замыкание предикатов
- Примеры правил
- $a = b ∧ b = c ⇒ a = b ∧ b = c ∧ a = c$
- $a > b ∧ b = c ⇒ a > b ∧ b = c ∧ a > c$
- $a > b ∧ b > c ⇒ a > b ∧ b > c ∧ a > c$
- Пример
- $σ_{P_1.p > P_2.p ∧ P_2.p ≥ 60}(P_1 ⋈_{P_1.SId = P_2.SId} P_2) ⇒$
- $σ_{P_1.p > P_2.p ∧ P_2.p ≥ 60 ∧ P_1.p > 60}(P_1 ⋈_{P_1.SId = P_2.SId} P_2) ⇒$
- $σ_{P_1.p > P_2.p}(σ_{p > 60}(P_1) ⋈_{P_1.SId = P_2.SId} σ_{p ≥ 60}(P_2))$
КНФ и ДНФ
- Преобразование предикатов
- Конъюнктивная нормальная форма
- Дизъюнктивная нормальная форма
- Вычисление КНФ
- Слева направо, до первой лжи
- Вычисление ДНФ
- Слева направо, до первой истины
Семантические оптимизации
Семантическая оптимизация
Применение знания об ограничениях
Неэквивалентные запросы
Тот же результат
Пример
$π_{FirstName}(Students ⋈ Groups) ⇒ π_{FirstName}(Students)$, если $Students.GId ⊂ Groups.GId$
Пример оптимизации
Ограничение
У всех, кто получает стипендию все оценки ≥60
check not HasScolarship or 60 <= all (select Points from Points where Points.SId = Id)
Запрос
Оценки стипендиатов группы M34391 по СУБД
select Points from Students natural join Points where HasScolarship and CId = 10 and GId = M34391
$σ_{HasScolarship ∧ CId = 10}(Students ⋈ Points)$
Оптимизированный запрос
$σ_{GId=M34391 ∧ HasScolarship}(Students) ⋈⋈ σ_{60 ≥ Points ∧ CId = 10}(Points)$