Приблизительный подсчет числа вхождений

Эта статья находится в разработке!

Задача о приблизительном подсчете числа вхождений: пусть дан некоторый поток данных [math]S = s_1, s_2, \dots, s_i, \dots, \: s_j \in U[/math]. Необходимо подсчитать, сколько раз элемент [math]x \in U[/math] встретился в потоке [math]S[/math] на момент времени [math]t[/math], т.е. [math]\sum_{j=1}^{t} I(s_j = x)[/math]. В данной статье рассмотрены две структуры данных, позволяющие решить эту задачу: Count-Min Sketch и Count Sketch. Обе структуры данных были предложены в начале 00-х в ответ на необходимость сбора информации об увеличившемся потоке интернет-трафика.

Постановка задачи

Рассмотрим постановку задачи о потоке данных. Пусть дан вектор [math]a[/math] размерности [math]n[/math]. Пусть состояние вектора в момент [math]t[/math] задано как [math]a(t) = [a_1(t), a_2(t), \dots, a_n(t)][/math] и [math]a(0) = [0, 0, \dots, 0][/math]. Зададимся потоком пар [math](i_1, c_1), (i_2, c_2), \dots, (i_m, c_m), \dots[/math] и будем обновлять вектор [math]a[/math] следующим образом:

[math] a_{i_t}(t) \leftarrow a_{i_t}(t-1) + c_t, [/math]

[math] a_{i’}(t) \leftarrow a_{i’}(t-1) \:\:\: \forall i’ \neq i_t. [/math]

В любой момент времени может поступить запрос о подсчете некоторой функции от [math]a(t)[/math]. Для задачи о приблизительном подсчете числа вхождений нас интересует запрос об оценке значения [math]a_{i}(t)[/math] для заданного [math]i[/math] в момент времени [math]t[/math] (англ. point query).

Для удобства [math]t[/math] будет опущена и мы будем использовать [math]a_i[/math] для обращения к текущему состоянию вектора.

Простым решением задачи может быть хранение вектора [math]a[/math] в явном виде. Однако при больших [math]n[/math] этот подход становится невыгодным из-за большего количества памяти, требуемого для хранения вектора [math]a[/math]. Хорошее решение данной задачи должно обладать следующими свойствами:

• оно должно требовать [math]O(polylog \: n)[/math] памяти;
• обновление [math]a[/math] и обработка запросов должны выполняться быстро и быть достаточно точными.

Ниже рассмотрены две структуры данных, позволяющие решить задачу о приблизительном подсчете числа вхождений, которые соответствуют этим требованиям.

Count-Min Sketch

Рисунок 1 — Процедура обновления Count-Min Sketch.

Count-Min Sketch (CM Sketch) это вероятностная структура данных, предложенная Г. Кормоудом (англ. G. Cormode) и С. Мутукришнаном (англ. S. Muthukrishnan) в 2003 году. Рассмотренный в этом разделе подход позволяет оценить [math]a_{i}[/math] при [math]c_j \geq 0 \:\: \forall j[/math]. CM Sketch может также быть применен для оценки [math]a_{i}[/math] когда существуют [math]c_j \lt 0[/math], а также для алгоритмов оценки скалярного произведения (англ. inner product query) и суммы промежутка величин [math]a_{l}, a_{l+1}, \dots, a_{r}[/math] (англ. range query).

Структура данных. CM Sketch с параметрами [math](\varepsilon, \delta)[/math] — это структура данных, которая включает в себя двумерный массив шириной [math]w = \lceil \frac{e}{\varepsilon} \rceil[/math] и глубиной [math]d = \lceil \ln \frac{1}{\delta} \rceil[/math]: [math]count[1, 1], count[1, 2], \dots, count [d, w][/math], а также [math]d[/math] попарно независимых хэш-функций из универсального семейства:

[math] h_1, h_2, \dots, h_d : \{1, \dots, n\} \rightarrow \{1, \dots, w\}. [/math]

В начале работы массив инициализируется нулями.

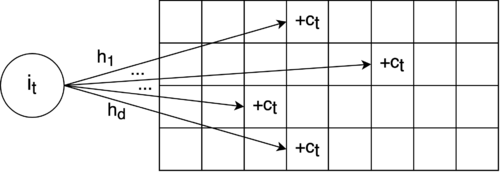
Обновление. При получении из потока пары [math](i_t, c_t)[/math], т.е. при увеличении величины [math]a_{i_t}[/math] на значение [math]c_t[/math], для каждой строки [math]j[/math] двумерного массива [math]count[/math] мы увеличиваем значение соответствующего счетчика, заданного хэш-функцией [math]h_j[/math]:

[math] count[j, h_j(i_t)] \leftarrow count[j, h_j(i_t)] + c_t \:\: \forall j. [/math]

Данная процедура описывается на рис. 1.

Ответ на запрос. Оценка значения [math]a_{i}[/math] подсчитывается как [math]\hat{a}_i = \min_j count[j, h_j(i)][/math].

Теорема (1):

Оценка [math]\hat{a}_i[/math] удовлетворяет [math]a_i \leq \hat{a}_i[/math], и с вероятностью как минимум [math]1 - \delta[/math] удовлетворяет [math] \hat{a}_i \leq a_i + \varepsilon ||\mathbf{a}||_1. [/math]

Доказательство:

[math]\triangleright[/math]

Рассмотрим хэш-функцию [math]h_j[/math] и счетчик [math]count[j, h_j(i)][/math], в который записываются обновления для элемента [math]a_i[/math]. Так как мы рассматриваем случай для [math]c_t \geq 0 \:\:\forall t[/math] и так как может существовать [math]a_k: h_j(i) = h_j(k), k \neq i[/math], то [math]a_i \leq \hat{a}_i[/math]. Оценим размер ошибки, накапливающийся в [math]count[j, h_j(i)][/math]. Зададимся индикаторной величиной [math]I_{i,j,k}[/math], равной единице если [math](i \neq k) \land (h_j(i) = h_j(k))[/math] и нулю в противном случае. Так как хэш-функции попарно независимы, получаем [math] E(I_{i,j,k}) = Pr[h_j(i) = h_j(k)] \leq \frac{1}{range(h_j)} = \frac{\varepsilon}{e}, [/math] где [math]range(h_j)[/math] — размер интервала значений, которые может принимать хэш-функция [math]h_j[/math]. Обозначим размер ошибки, накапливающийся в [math]count[j, h_j(i)][/math] как случайную величину [math]X_{i,j} = \sum_{k=1}^{n} I_{i,j,k}a_k[/math], т.е. [math]count[j, h_j(i)] = a_i + X_{i,j}[/math]. В таком случае [math] E(X_{i,j}) = E(\sum_{k=1}^{n} I_{i,j,k}a_k) = \sum_{k=1}^{n} E(I_{i,j,k}a_k) = \sum_{k=1}^{n} a_k E(I_{i,j,k}) \leq \frac{\varepsilon}{e} \sum_{k=1}^{n} a_k = \frac{\varepsilon}{e} || \mathbf{a} ||_1. [/math] Наконец, докажем что [math]Pr[\hat{a}_i \gt a_i + \varepsilon ||\mathbf{a}||_1][/math] не превышает [math]\delta[/math], из чего следует, что [math]Pr[\hat{a}_i \leq a_i + \varepsilon ||\mathbf{a}||_1] \gt 1 - \delta[/math]. [math]Pr[\hat{a}_i \gt a_i + \varepsilon ||\mathbf{a}||_1] = Pr[\forall j \: count[j, h_j(i)] \gt a_i + \varepsilon ||\mathbf{a}||_1] = Pr[\forall j \: a_i + X_{i,j} \gt a_i + \varepsilon ||\mathbf{a}||_1] = Pr[\forall j \: X_{i,j} \gt e E(X_{i,j})] [/math] [math]=^{(1)} Pr[X_{i,1} \gt e E(X_{i,1}) \times \dots \times X_{i,d} \gt e E(X_{i,d})] \leq^{(2)} e^{-d} \leq \delta,[/math] где [math](1)[/math] вытекает из попарной независимости хэш-функций, а [math](2)[/math] — из неравенства Маркова.

[math]\triangleleft[/math]

Count Sketch

Count Sketch — вероятностная структура данных, предложенная М. Чарикаром (англ. M. Charikar), К. Ченом (англ. K. Chen) и М. Фара-Колтоном (англ. M. Farach-Colton) в 2002 году. В отличие от Count-Min Sketch, эта структура данных позволяет оценивать [math]a_{i}[/math] даже для отрицательных [math]c_t[/math].

Структура данных. Пусть [math]h_1, h_2, \dots, h_d[/math] и [math]s_1, s_2, \dots, s_d[/math] — это наборы хэш-функций, принадлежащие универсальному семейству и удовлетворяющие

[math] h_1, h_2, \dots, h_d : \{1, \dots, n\} \rightarrow \{1, \dots, w\}, [/math]

[math] s_1, s_2, \dots, s_d : \{1, \dots, n\} \rightarrow \{-1, 1\}. [/math]

Count Sketch включает в себя двумерный массив шириной [math]w[/math] и глубиной [math]d[/math]: [math]count[1, 1], count[1, 2], \dots, count [d, w][/math], а также хэш-функции [math]h_1, h_2, \dots, h_d[/math] и [math]s_1, s_2, \dots, s_d[/math]. В начале работы массив инициализируются нулями.

Обновление. При получении из потока пары [math](i_t, c_t)[/math], для каждой строки [math]j[/math] двумерного массива [math]count[/math] мы обновляем значение соответствующего счетчика, заданного хэш-функцией [math]h_j[/math], следующим образом:

[math] count[j, h_j(i_t)] \leftarrow count[j, h_j(i_t)] + c_t \cdot{} s_j(i_t) \: \forall j. [/math]

Ответ на запрос. Оценка значения [math]a_{i}[/math] подсчитывается как

[math]\hat{a}_i = median_j \{count[j, h_j(i)] \cdot{} s_j(i) \}[/math].

Теорема (2):

Оценка значения [math]a_{i}[/math] полученная с помощью Count Sketch удовлетворяет [math] a_{i} - \sqrt{\frac{3}{R}} ||\mathbf{a}||_2 \leq \hat{a}_i \leq a_{i} + \sqrt{\frac{3}{R}} ||\mathbf{a}||_2. [/math]

Доказательство:

[math]\triangleright[/math]

Воспользуемся схемой доказательства, сходной с той, что была использована для Count-Min Sketch. С учетом коллизий хэш-функций получаем значение, хранимое в счетчике [math]count[j, h_j(i)][/math]: [math] count[j, h_j(i)] = \sum_{k=1}^{n} \big(I_{h(i)=h(k)} \cdot{} a_k \cdot{} s_j(k)\big) = a_i \cdot{} s_j(i) + \sum_{k=1, k \neq i}^{n} \big(I_{h(i)=h(k)} \cdot{} a_k \cdot{} s_j(k)\big), [/math] из чего следует, что [math] s_j(i) \cdot{} count[j, h_j(i)] = a_i \cdot{} s_j(i)^2 + \sum_{k=1, k \neq i}^{n} \big(I_{h(i)=h(k)} \cdot{} a_k \cdot{} s_j(k) \cdot{} s_j(i) \big). [/math] Схоже с предыдущим доказательством [math] E(I_{h(i)=h(k)}) \leq \frac{1}{range(h_j)} = \frac{1}{w}. [/math] Кроме того, очевидно, что [math] E(s_j(i)) = 0, [/math] [math] E(s_j(i))^2 = 1. [/math] Найдем матожидание [math]E(s_j(i) \:count[j, h_j(i)])[/math]: [math] E(s_j(i) \:count[j, h_j(i)]) = a_i \cdot{} E(s_j(i)^2) + \sum_{k=1, k \neq i}^{n} \big(E(I_{h(i)=h(k)}) \cdot{} a_k \cdot{} E(s_j(k)) \cdot{} E(s_j(i)) \big) = a_i \cdot{} E(s_j(i)^2) = a_i. [/math] Так как в отличие от Count-Min Sketch, Count Sketch может работать при [math]c_t \lt 0[/math], мы не можем использовать неравенство Маркова. Вместо этого воспользуемся неравенством Чебышёва, для чего подсчитаем дисперсию: [math] Var(s_j(i) \:count[j, h_j(i)]) = E\Big[(s_j(i) \cdot{} count[j, h_j(i)] - a_i)^ 2\Big] [/math] [math] = E\Big[(a_i \cdot{} s_j(i)^2 + \sum_{k=1, k \neq i}^{n} \big(I_{h(i)=h(k)} \cdot{} a_k \cdot{} s_j(k) \cdot{} s_j(i) \big) - a_i) ^ 2\Big] [/math] [math] = E\Big[\Big(\sum_{k=1, k \neq i}^{n} \big(I_{h(i)=h(k)} \cdot{} a_k \cdot{} s_j(k) \cdot{} s_j(i) \big)\Big) ^ 2\Big] [/math] [math] = E\Big[\sum_{k=1, k \neq i}^{n} \big(I_{h(i)=h(k)}^2 \cdot{} a_k^2 \cdot{} s_j(k)^2 \cdot{} s_j(i) ^2\big) + \sum_{k \neq i, l \neq i} \big(I_{h(i)=h(k)} \cdot{} I_{h(i)=h(l)} \cdot{} a_k \cdot{} a_l \cdot{} s_j(k) \cdot{} s_j(l) \cdot{} s_j(i) ^2\big)\Big] [/math] [math] = E\Big[\sum_{k=1, k \neq i}^{n} \big(I_{h(i)=h(k)} \cdot{} a_k^2 \big)\Big] = \frac{1}{w} \sum_{k=1, k \neq i}^{n} a_k^2 = \frac{||\mathbf{a}||_2^2}{w}. [/math] Подставим полученную дисперсию в неравенство Чебышёва для [math]k = \sqrt{3}[/math]: [math] Pr\Big[(s_j(i) \cdot{} count[j, h_j(i)] - a_i) \gt \sqrt{\frac{3}{w}}||\mathbf{a}||_2\Big] \lt \frac{1}{3}. [/math]

[math]\triangleleft[/math]

Применение

С момента появления Count-Min Sketch и Count Sketch эти структуры данных стали широко использоваться для подсчета статистики, например, для отслеживания популярности контента среди разных групп пользователей. Рассмотрим пример с подсчетом числа просмотров для твита. Отслеживание всех просмотров на разных веб-сайтах результируется в большом потоке данных, которым сложно управлять. Кроме того, ситуация, когда твит наберет большое число просмотров на одной платформе и окажется незамеченным на других, маловероятна, поэтому разработчики могут не волноваться об излишней точности подсчетов. Использование скетча для каждого отдельного твита занимает ненамного больше места чем само сообщение и метаданные о нем, но при этом позволяет отслеживать, какие платформы привлекают больше всего читателей с хорошей точностью.

Кроме того, скетчи также популярны в телекоммуникационных сетях, через узлы которых проходит большое количество трафика, которое не может быть сохранено в явном виде. Сбор статистики о распределении трафика в сети позволяет эффективно управлять ею, снижая загруженность критических узлов.

Описанные выше скетчи также могут быть использованы для решения задачи выявления наиболее часто встречающихся элементов (англ. heavy hitters). Это может быть актуально, например, для поисковых систем, таких как Google. Подробное описание решения этой задачи с помощью Count-Min Sketch и Count Sketch описано в оригинальных статьях.

См. также

• Хеш-таблица
• Универсальное семейство хеш-функций
• Анализ социальных сетей

Источники информации

• Graham Cormode, S. Muthukrishnan, "An Improved Data Stream Summary: The Count-Min Sketch and its Applications", 2003 [1]
• Barna Saha, "Algorithmic Techniques for Big Data. Lecture 2" [2]
• Moses Charikar, Kevin Chen, Martin Farach-Colton, "Finding Frequent Items in Data Streams", 2002 [3]
• Anshumali Shrivastava, "Probabilistic Algorithms and Data Structure. Lecture 10" [4]
• Graham Cormode, "What is Data Sketching, and Why Should I Care?", 2017 [5]