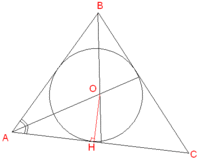
Формулировка
Пусть треугольник задан двумя векторам [math]\overrightarrow{AB}[/math] и [math]\overrightarrow{AC}[/math]. Необходимо найти центр и радиус вписанной окружности
Решение
Сначала найдем радиус окружности. Площадь треугольника [math]ABC[/math] мы можем найти из векторного произведения векторов [math]\overrightarrow{AB}[/math] и [math]\overrightarrow{AC}[/math]. С другой стороны, [math]S_{ABC} = S_{AOB} + S_{AOC} + S_{BOC}[/math]. А площадь маленьких треугольников равна половине произведения радиуса окружности на основание. Например, [math]S_{AOC} = \frac{1}{2} * R * AC[/math]. Отсюда получаем выражение, из которого можно найти радиус окружности. [math]R = \frac{|[\overrightarrow{AB} \times \overrightarrow{AC}]|}{AB + BC + AC}[/math]
Теперь будем искать центр окружности. Как известно, центр вписанной окружности лежит на пересечении биссектрис. Вектор, коллиниарный вектору [math]\overrightarrow{AO}[/math], можно найти следующим образом [math]\overrightarrow{l} = \frac{\overrightarrow{AB}}{AB} + \frac{\overrightarrow{AC}}{AC}[/math]. Обозначим вектор [math]\overrightarrow{l_1} = \frac{\overrightarrow{l}}{|\overrightarrow{l}|} [/math]. Теперь необходимо найти длину вектора [math]\overrightarrow{AO}[/math]. [math] AO = \frac{OH}{sin\frac{\alpha}{2}}[/math], где [math]\alpha = \angle{BAC}[/math]. По формуле понижения степени [math] sin^{2}\frac{\alpha}{2} = \frac{1 - cos\alpha}{2}[/math]. Найти [math]cos\alpha[/math] можно из скалярного произведения. [math]cos\alpha = \frac{(\overrightarrow{AB};\overrightarrow{AC})}{|\overrightarrow{AB}||\overrightarrow{AC}|}[/math]. Заметим, что [math]OH = R[/math], и можем выразить длину [math]AO = \frac{|[\overrightarrow{AB} \times \overrightarrow{AC}]|}{AB + BC + AC}\frac{\sqrt{2}|\overrightarrow{AB}||\overrightarrow{AC}|}{|\overrightarrow{AB}||\overrightarrow{AC}| - (\overrightarrow{AB};\overrightarrow{AC})}[/math]. Задача почти решена, осталось только отметить, что [math]AB = |\overrightarrow{AB}|, AC = |\overrightarrow{AC}|, BC = |\overrightarrow{AB} - \overrightarrow{AC}|[/math], а радиус-вектор точки центра окружности совпадает с радиус-вектором [math]\overrightarrow{AO} [/math], a [math]\overrightarrow{AO} = \overrightarrow{l_1} * AO [/math]