Граф замен

Теорема:

Пусть [math]M_1 = \lt X, I_1\gt [/math] и [math]M_2 = \lt X, I_2\gt [/math] - матроиды с ранговыми функциями [math]r_1[/math] и [math]r_2[/math], соответственно. Тогда максимальная мощность множества из [math]I_1 \cap I_2[/math] равна [math]\min_{U \subset X} (r_1(U) + r_2(X \setminus U))[/math].

Доказательство:

[math]\triangleright[/math]

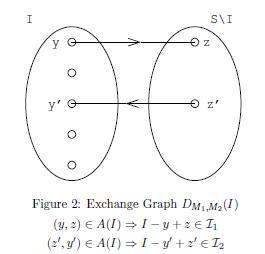
Пусть [math]I \in I_1 \cap I_2[/math]. Следовательно, [math]\forall U \subset X[/math] верно [math]I \cap U \in I_1, I \setminus U \in I_2[/math]. Тогда, из определения ранга, [math]|I| = |I \cap U| + |I \setminus U| \leq r_1(U) + r_2(X \setminus U)[/math]. В другую сторону докажем теорему алгоритмически. На каждом этапе алгоритм получает [math]I \in I_1 \cap I_2[/math] и либо заключает, что множества большей мощности из [math]I_1 \cap I_2[/math] получить нельзя, либо возвращает [math]J \in I_1 \cap I_2: |J| = |I| + 1[/math]. Введем двудольный ориентированный граф замен для [math]M_1[/math] и [math]M_2[/math] - граф [math]D[/math]. Левой долей [math]D[/math] являются элементы текущего множества [math]I \in I_1 \cap I_2[/math], правой - все остальные элементы [math]X \setminus I[/math]. Проведем ребра [math](y, z): y \in I, z \in X \setminus I, I \setminus y \cup z \in I_1[/math], а также [math](z', y'): y' \in I, z' \in X \setminus I, I \setminus y' \cup z' \in I_2[/math]. Пусть [math]X_1 = \{z \in X \setminus I | I \cup z \in I_1 \}, X_2 = \{z \in X \setminus I | I \cup z \in I_2 \}, P[/math] - кратчайший путь в [math]D[/math] из [math]X_1[/math] в [math]X_2[/math]. Тогда алгоритм с помощью этого пути либо определяет максимальность набора [math]I[/math], либо позволяет найти набор большей мощности.

[math]\triangleleft[/math]