Алгоритм Флойда
Алгоритм Флойда (алгоритм Флойда–Уоршелла) — динамический алгоритм нахождения длин кратчайших путей между всеми парами вершин взвешенного ориентированного графа. Разработан в 1962 году.
Алгоритм
Пусть дан граф ; ; вершины пронумерованы от до .
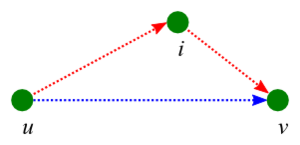
Обозначим длину кратчайшего пути между вершинами и , содержащего, помимо самих вершин и , только вершины с номерами как . Понятно, что .
На каждом шаге алгоритма, мы будем брать очередную вершину (пусть, её номер ) и для всех пар вершин и вычислять . Т.е., если кратчайший путь из в , содержащий только вершины с номерами , проходит через вершину , то пройдём сначала из в , затем из в , иначе ничего менять не будем.
Код (в первом приближении)
# Инициализация
d[0] = w
# Основная часть
for i in {1..n}:
for u in {1..n}:
for v in {1..n}:
d[i][u][v] = min(d[i-1][u][v], d[i-1][u][i] + d[i-1][i][v])
Код (окончательный)
Можно обойтись без первого индекса в массиве, т.е. использовать двумерный массив . В процессе работы алгоритма поддерживается инвариант , а значит тоже в итоге сойдутся к решению.
# Инициализация
d = w
# Основная часть
for i in {1..n}:
for u in {1..n}:
for v in {1..n}:
d[u][v] = min(d[u][v], d[u][i] + d[i][v])
Алгоритм всегда завершит работу за — как несложно видеть, три вложенных цикла выполняются по раз каждый.
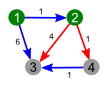
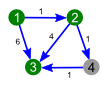
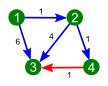
Пример работы
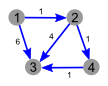 |
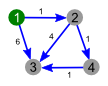 |
 |
 |
|
Вывод кратчайшего пути
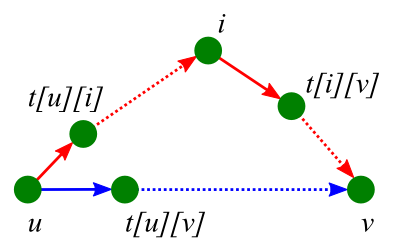
Алгоритм Флойда легко модифицировать таким образом, чтобы он возвращал не только длину кратчайшего пути, но и сам путь. Для этого достаточно завести дополнительный массив , в котором будет храниться номер вершины, в которую надо пойти следующей, чтобы дойти из в по кратчайшему пути.
Модифицированный алгоритм
# Инициализация
d = w
t[u][v] = v если есть ребро uv
# Основная часть
for i in {1..n}:
for u in {1..n}:
for v in {1..n}:
if (d[u][i] + d[i][v]) < d[u][v]:
d[u][v] = d[u][i] + d[i][v]
t[u][v] = t[u][i]
# Вывод кратчайшего пути
def get_shortest_path(u, v):
if d[u][v] == inf:
raise NoPath # Из u в v пути нет
c = u
while c != v:
yield c
c = t[c][v]
yield v
Литература
- Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест, Рональд Л., Штайн Клиффорд Алгоритмы: построение и анализ, 2-е издание. Пер. с англ. — М.:Издательский дом "Вильямс", 2010. — 1296 с.: ил. — Парал. тит. англ. — ISBN 978-5-8459-0857-5 (рус.)