Материал из Викиконспекты
| Определение: |
| Недетерминированный конечный автомат (НКА) — это пятерка [math]\langle \Sigma , Q, s \in Q, T \subset Q, \delta : Q \times \Sigma \to 2^Q \rangle[/math], где [math]\Sigma[/math] — алфавит, [math]Q[/math] — множество состояний автомата, [math]s[/math] — начальное состояние автомата, [math]T[/math] — множество допускающих состояний автомата, [math]\delta[/math] — функция переходов.
Таким образом единственное отличие НКА от ДКА — это существование нескольких переходов по одному символу из одного состояния. |
| Определение: |
| Мгновенная кофигурация — |
- [math]\langle q, \alpha \rangle \vdash \langle p, \beta \rangle[/math], если:
- [math]\alpha = c\beta[/math]
- [math]p \in \delta (q, c)[/math]
- [math]\langle q, \alpha \rangle \vdash^* \langle p, \beta \rangle[/math], если [math]\exists n[/math]:
- [math]\langle q, c_1 c_2 c_3 ...c_n\beta \rangle \vdash \langle u_1, c_2 c_3 ...c_n\beta \rangle \vdash \langle u_2, c_3 ...c_n\beta \rangle ...\vdash \langle u_{n-1}, c_n\beta \rangle \vdash \langle p, \beta \rangle[/math]
Автомат допускает слово [math]\alpha[/math], если [math]\exists t \in T: \langle s, \alpha \rangle \vdash^* \langle t, \varepsilon \rangle[/math].
Процесс допуска происходит так же, как в ДКА, в котором Мерлин помогает выбрать правильный переход.
Язык автомата
| Определение: |
| [math]L(\mathcal{A})=\{\alpha| \exists t: \langle s, \alpha \rangle \vdash^* \langle t, \varepsilon \rangle t \in T\}[/math] --- язык автомата [math]\mathcal{A}[/math]. |
Пример
Автомат, допускающий слова над алфавитом из символов 0 и 1, допускающий слова оканчивающиеся на 0101.
(0|1)*0101
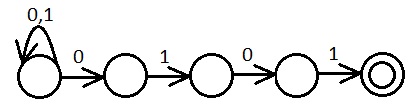
Способ хранения
Алгоритм определяющий допустимость автоматом слова
См. также
