Двоичный каскадный сумматор
Версия от 00:21, 17 ноября 2011; Bobrov (обсуждение | вклад)
| Определение: |
| Двоичный каскадный сумматор — цифровая схема, осуществляющая сложение двух многоразрядных двоичных чисел. |
Принцип работы
Обозначения:
- — i-ый разряд суммируемых чисел
- — биты переноса
- — результат сложения.
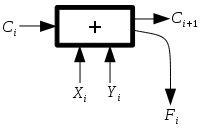
Рассмотрим один элемент линейного каскадного сумматора. В некоторых случаях бит переноса зависит только от значений и :
- Generate(g): , тогда
- Kill(k): , тогда ,
- Propagate(p): , тогда ,
Обозначим композицию действий над переносами значком и рассмотрим таблицу:
| k | p | g | |
|---|---|---|---|
| k | k | k | g |
| p | k | p | g |
| g | k | g | g |
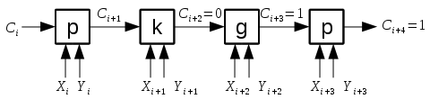
Пример
Таким образом, функцию можно определить как последнее не "P".
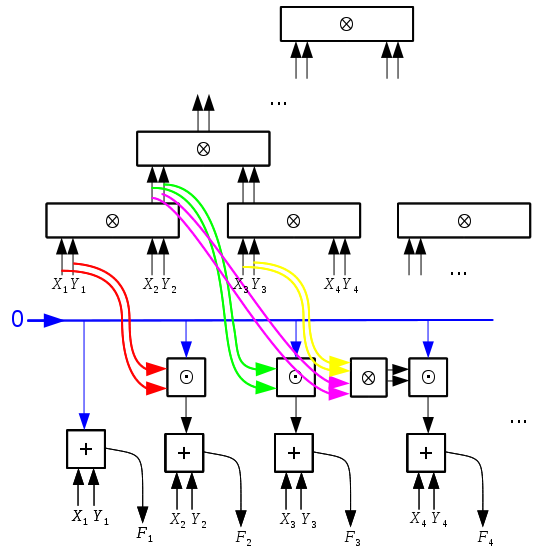
Схема
Сумматор состоит из двух частей. Первая часть — это группа полных сумматоров, вычисляющих ответ. Вторая часть — дерево отрезков, с помощью которого вычисляется бит переноса.
Обозначения
- — полный сумматор, вычисляет результат сложения.
- вычисляет композицию двух переносов.
- возвращает , старший бит сумматора.
Схемная сложность
Дерево отрезков вычисляет биты переноса за , оставшиеся действия выполняются за . Суммарное время работы — .