Интерактивные протоколы. Класс IP. Класс AM

Класс IP

Определение:

[math]IP[f] = \{L|\exists \langle V, P \rangle : [/math] [math] 1) \forall x \in L \Rightarrow P(V(x) = 1) \ge \frac{2}{3} [/math] [math] 2) \forall x \notin L \Rightarrow P(V(x) = 1) \le \frac{1}{3} [/math] [math] 3) [/math] Число раундов интерактивного протокола [math] f(n), n = |x| [/math]

Теорема:

[math]\mathrm{NP} \subset \mathrm{IP[1]}[/math]

Доказательство:

[math]\triangleright[/math]

[math]\mathrm{NC^i} \subset \mathrm{AC^i}[/math] Это понятно из определения [math]\mathrm{NC^i}[/math] и [math]\mathrm{AC^i}[/math]. [math]\mathrm{AC^i} \subset \mathrm{NC^{i+1}}[/math] Пусть [math]L \in \mathrm{AC^i}[/math]. [math]L[/math] распознается семейством схем [math]C_n[/math] полиномиального размера. Значит, степень входа элементов схемы [math]C_n[/math] — это полином от [math]n[/math]. 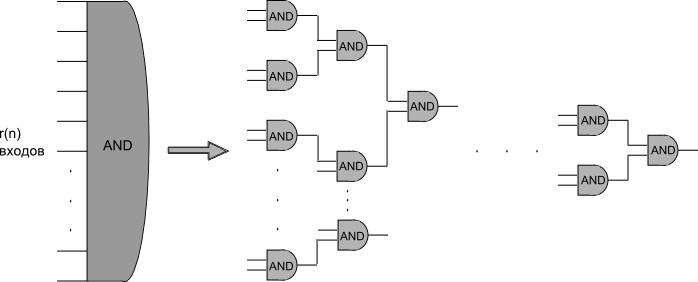Заменим элементы схемы [math]C_n[/math] элементами со степенью входа не более двух следующим образом: При замене каждого такого элемента глубина схемы увеличивается не более чем в [math]log_2 r(n) = O(log(n))[/math], а так как изначально глубина схемы была [math]O(log^i(n))[/math], то после замены всех элементов глубина схемы станет [math]O(log^i(n)) \cdot O(log(n)) = O(log^{i+1}(n))[/math]. Так как при замене элемента мы добавляем не более [math]r(n)[/math] элементов, а изначально размер схемы был полиномиальным и каждый ее элемент мы заменили на полином элементов, то после всех замен размер схемы остался полиномиальным.

[math]\triangleleft[/math]